Lab Week 06: More on Mandelbrot

The Mandelbrot Set

Mandelbrot Set

• Fix a complex number $c = a + b i$
• Form sequence $z_1, z_2, \ldots$
  • $z_1 = c$
  • $z_n = z_{n-1}^2 + c$ ($n > 1$)
• Mandelbrot set is the set of $c$ such that the sequence $z_1, z_2, \ldots$ remains bounded (i.e., $|z_n|$ does not grow indefinitely)

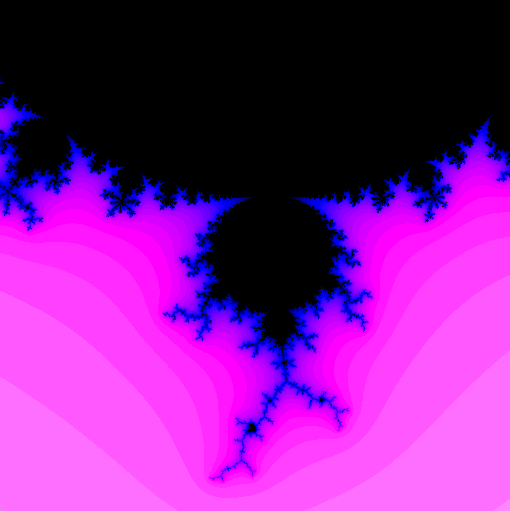
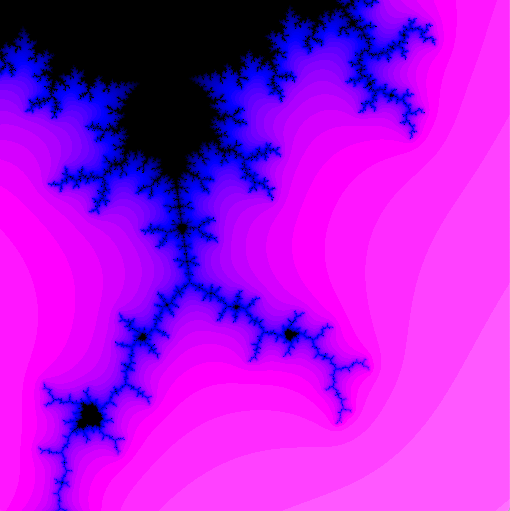
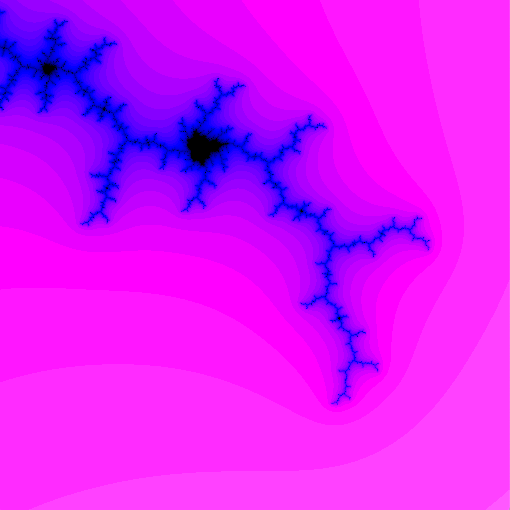
Mandelbrot Set Plotted

Computing the Mandelbrot Set

Choose parameters:

• $N$ number of iterations
• $M$ maximum modulus

Given a complex number $c$:

• compute $z_1 = c, z_2 = z_1^2 + c,\ldots$ until
  1. $|z_n| \geq M$
     • stop because sequence appears unbounded
  2. $N$th iteration
     • stop because sequence appears bounded
• if $N$th iteration reached $c$ is likely in Mandelbrot set

Illustration

Drawing the Mandelbrot Set

• Choose a region consisting of $a + b i$ with
  • $x_{min} \leq a \leq x_{max}$
  • $y_{min} \leq b \leq y_{max}$
• Make a grid in the region
• For each point in grid, determine if in Mandelbrot set
• Color accordingly

Counting Iterations

Given a complex number $c$:

• compute $z_1 = c, z_2 = z_1^2 + c,\ldots$ until
  1. $|z_n| \geq M$
     • stop because sequence appears unbounded
  2. $N$th iteration
     • stop because sequence appears bounded
• if $N$th iteration reached $c$ is likely in Mandelbrot set

Color by Escape Time

1. Color black in case 2 (point is in Mandelbrot set)
2. Change color based on $n$ in case 1:
   • smaller $n$ are “farther” from Mandelbrot set
   • larger $n$ are “closer”

Why Thread Pools?

Partitions?

Your Task

Basic task:

• Use executor framework to compute Mandelbrot set as quickly as possible!
• Make a color map

Going Farther:

• Animate zoom

Defining a Color Map

Parameters:

• $M$ maximum modulus
• $N$ number of iterations

Record:

• Number of iterations until escape, or
• Indicate no escape (point is in Mandelbrot set)

More Formally

Compute float esc[][] a height by width 2d array:

• esc[i][j] stores a “normalized escape time” of pixel i,j:
  • 0.0 <= esc[i][j] <= 1.0
  • esc[i][j] == 0.0 indicates point in Mandelbrot set
  • esc[i][j] == 1.0 indicates escape time of 0 ($\mid c\mid \geq M$)
• Color map associates a color to each value of esc

What To Code:

• Complete MandelbrotFrame.java
• Write separate class MTask