Lab Week 05: Executors and Fractals

Announcements

I owe you feedback!
Homework 02 posted, due Friday
- fairly brief (3 questions)
Accountability groups

Outline

Threads and Executors
The Mandelbrot Set
Lab 03: Drawing the Mandelbrot Set

Previously

Created Threads and ran them in parallel
- implmenet Runnable interface
- create and start instances
- join to wait until threads finish

Drawbacks

Creating new Threads has significant overhead
- best performance by balancing number of threads/processors available
Need to explicitly partition into relatively few pieces
- partitioning may be unnatural
- partition may be unbalanced:
  - don’t know in advance how long computations will take

When tasks are fairly homogenous (e.g., computing $\pi$, shortcuts) previous approach is good

A (Sometimes) Better Way

A nice Java feature: thread pools

Create a (relatively small) pool of threads
Assign tasks to the pool
Available threads process tasks
- if all threads occupied, tasks stored in a queue
- as threads are completed, threads in pool are reused

When are Thread Pools Better?

Many smaller tasks
Fixed partition of problem may be unbalanced
“Online” problems: set of tasks not known in advance
- e.g., processing requests for web server

Thread Pools in Java

Implement Executor interface
- void execute(Runnable command) method
More control of task handling: ExecutorService interface:
- submit tasks
- wait for tasks to complete
- shut down pool (don’t accept new tasks)

Built-in `ExecutorService` Implementations

From java.util.concurrent.Executors:

newFixedThreadPool(int nThreads)
- make a pool with a fixed number of threads
newSingleThreadExecutor()
- make a pool with a single thread
newCachedThreadPool()
- make pool that creates new threads as needed (reuses old if available)
…

Using Thread Pools 1

Define tasks

public class MyTask implements Runnable {
    ...
    public void run () {
        ...
    }
}

Using Thread Pools 2

Create a pool, e.g., fixed thread pool

int nThreads = ...;

ExecutorService pool = Exercutors.newFixedThreadPool(nThreads);

Create and execute tasks

MyTask task = new MyTask(...);

pool.execute(task);

Using Thread Pools 3

Shutting down the pool

pool.shutdown();

Wait for all pending processes to complete (like join() method)

try {

    pool.awaitTermination(Long.MAX_VALUE, TimeUnit.NANOSECONDS);

} catch (InterruptedException e) {

    // do nothing

}

Example

Shortcuts from Lab 02:

	for (int i = 0; i < size; ++i) {
	    for (int j = 0; j < size; ++j) {

		float min = Float.MAX_VALUE;
		
		for (int k = 0; k < size; ++k) {
		    float x = matrix[i][k];
		    float y = matrix[k][j];
		    float z = x + y;

		    if (z < min) {
			min = z;
		    }
		}

		shortcuts[i][j] = min;
	    }
	}

A Small Task

For fixed row i, col j:

		float min = Float.MAX_VALUE;
		
		for (int k = 0; k < size; ++k) {
		    float x = matrix[i][k];
		    float y = matrix[k][j];
		    float z = x + y;

		    if (z < min) {
			min = z;
		    }
		}
		shortcuts[i][j] = min;

Two Approaches

Approach 1:

Make a separate thread for each task
- need size * size threads

Approach 2:

Make a thread pool and let the pool decide
- choose pool size from availableProcessors()

Try it Yourself

Test Them

Which method is faster? How much?

How does pool performance compare to previous multithreaded version (without optimizing cache locality)?

The Mandelbrot Set

Complex Numbers

Recall:

the imaginary number $i$ satisfies $i^2 = -1$
complex numbers are number of the form $a + b i$ where $a$ and $b$ are real
complex arithmetic:
- $(a + b i) + (c + d i) = (a + c) + (b + d) i$
- $(a + b i) \cdot (c + d i) = (a c - b d) + (a d + b c) i$
modulus (or length):
- $|a + b i| = \sqrt{a^2 + b^2}$

Complex Plane

Associate complex number $a + b i$ with point $(a, b)$ in plane

Iterated Operations

Fix a complex number $c$

Define sequence $z_1, z_2, z_3, \ldots$ by
- $z_1 = c$
- for $n > 1$, $z_{n} = z_{n-1}^2 + c$
What happens for different values of $c$?

Mandelbrot Set

The Mandelbrot set is the set of complex numbers $c$ such that the sequence $z_1, z_2, \ldots$ remains bounded (i.e., $|z_n|$ does not grow indefinitely)

Computing the Mandelbrot Set

Choose parameters:

$N$ number of iterations
$M$ maximum modulus

Given a complex number $c$:

compute $z_1 = c, z_2 = z_1^2 + c,\ldots$ until
1. $|z_n| \geq M$
  - stop because sequence appears unbounded
2. $N$th iteration
  - stop because sequence appears bounded
if $N$th iteration reached $c$ is likely in Mandelbrot set

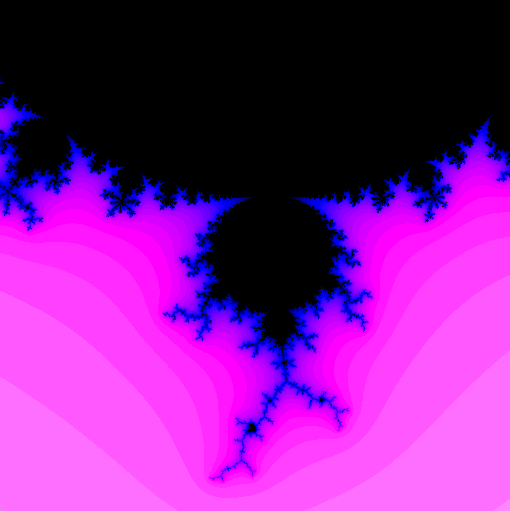
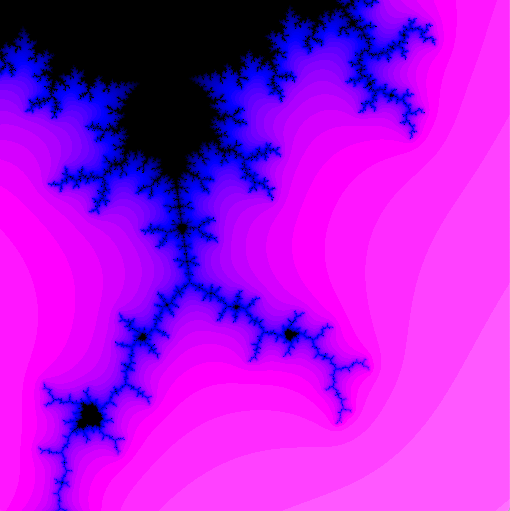
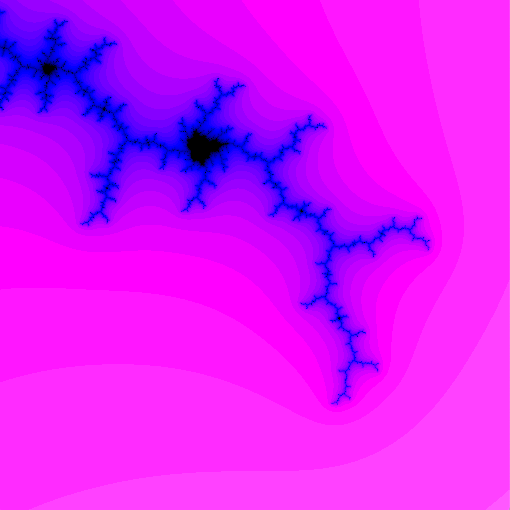
Illustration

Drawing the Mandelbrot Set

Choose a region consisting of $a + b i$ with
- $x_{min} \leq a \leq x_{max}$
- $y_{min} \leq b \leq y_{max}$
Make a grid in the region
For each point in grid, determine if in Mandelbrot set
Color accordingly

Counting Iterations