Lab 02: Computing Shortucts

A Network

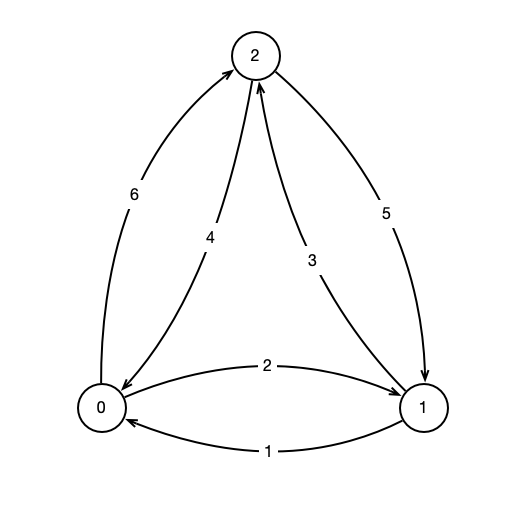
Network

• nodes and edges between nodes
  • nodes labeled $0, 1, \ldots, n$
  • directed edges $(i, j)$ from $i$ to $j$ for each $i \neq j$
• edges $(i, j)$ have associated weight, $w(i, j) \geq 0$
  • weight indicates cost or distance to move from $i$ to $j$

Shortcuts

What is cheapest path from 0 to 2?

A Problem

Given a network as above, for all $i \neq j$, find cheapest path of length (at most) 2 from $i$ to $j$

• weight of a path is sum of weight of edges
• convention: $w(i, i) = 0$
• a shortcut from $i$ to $j$ is a path $i \to k \to j$ where $w(i, k) + w(k, j) < w(i, j)$

Shortcut Distances

Representing Input

• \[D = \left( \begin{array}{ccc} 0 & 2 & 6\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right)\]

Computing Output

• $D = (d_{ij})$
• Output $R = (r_{ij})$
  • $r_{ij}$ = shortcut distance from $i$ to $j$
  • computed by \(r_{ij} = \min_k d_{ik} + d_{kj}\)

Example

• \[D = \left( \begin{array}{ccc} 0 & 2 & 6\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right)\]
• \[R = \left( \begin{array}{ccc} 0 & 2 & 5\\ 1 & 0 & 3\\ 4 & 5 & 0 \end{array} \right).\]

In Code

• Create a SquareMatrix object
• SquareMatrix stores a 2d array of floats called matrix
  • matrix[i][j] stores \(w(i, j)\)

Your Assignment

Write a program that computes shortcut matrix as quickly as possible!

• Today, you’ll code a baseline implementation
  • getShortcutMatrixBaseline()
• Your assignment is to optimize the code to write
  • getShortcutMatrixOptimized ()

Today

Working in small groups, write getShortcutMatrixBaseline()

Downloads:

• SquareMatrix.java
• MatrixTester.java