Lecture 25: Mazes and States
Last Time
- Considered solving mazes
- Developed depth-first strategy
- Saw depth-first can yield inefficient solutions
- Considered another strategy: breadth-first
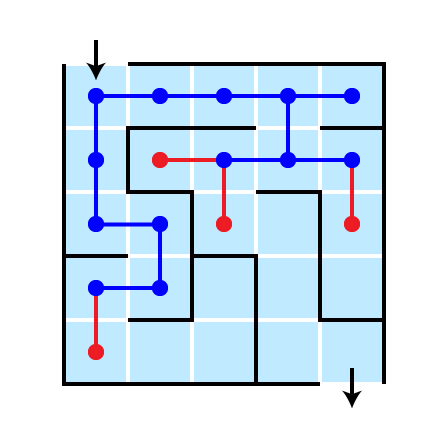
Another Strategy
Explore in all directions simultaneously!
- Consider all possible first steps
- Then all possible second steps
- ignore previously visited cells
- …
This strategy is breadth first
- Explore all possible next steps
Illustration: Depth 1
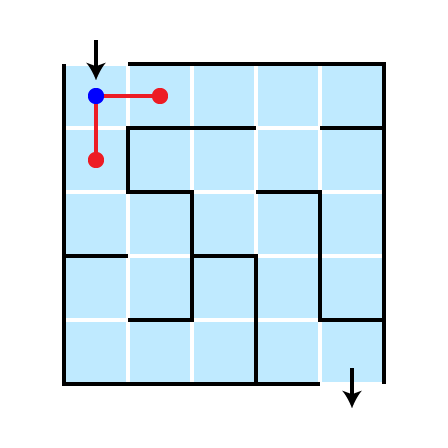
Illustration: Depth 2
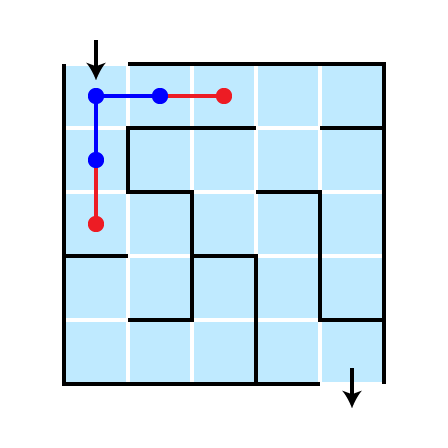
Illustration: Depth 3
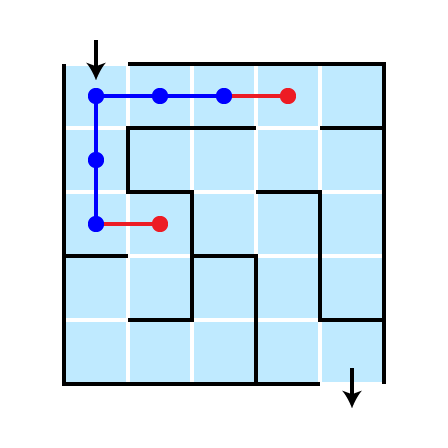
Illustration: Depth 4
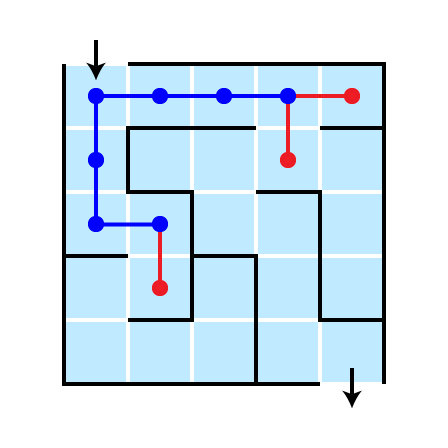
Completed Search
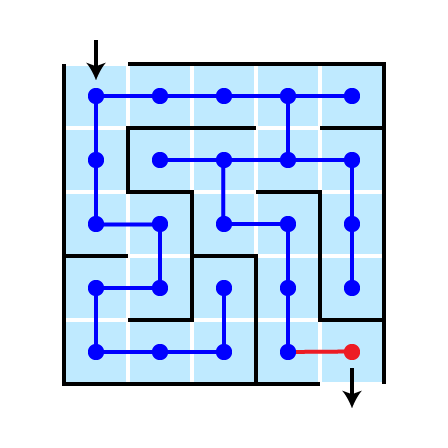
Return Solution
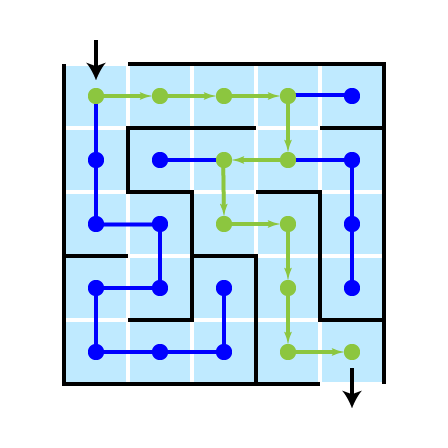
A Nice Feature
The shortest path from start to goal is found
- why?
Implementation Notes
- again, store
visitedandactivecells -
activecells are boundary betweenvisitedand unvisited - store
activecells in a queue- all cells at distance $d$ from start are visited before any cell at distance $d+1$ is visited
- initially,
activeandvisitedare just starting cell - each cell stores its
parentcell-
parentis cell from which cell was visited
-
Breadth-first Illustration
Breadth-first in Code
Two Solution Philosophies
- Depth-first
- Keep going until you can’t go any farther, then backtrack
- Naturally suited to stack ADT
- Naturally suited to recursive solution
- Breadth-first
- Exhaustively search all cells in increasing distance from start
- Keep track of “parent” cell for each cell
Abstracting Away from Mazes
Features of Mazes
- Comprised of cells: states
- Cells having neighboring cells
- can move from one cell to its neighbors
- moving from one state to another is a transition
- Have starting position
- Have goal position(s)
Objective: find a sequence of transitions from initial state to gaol state
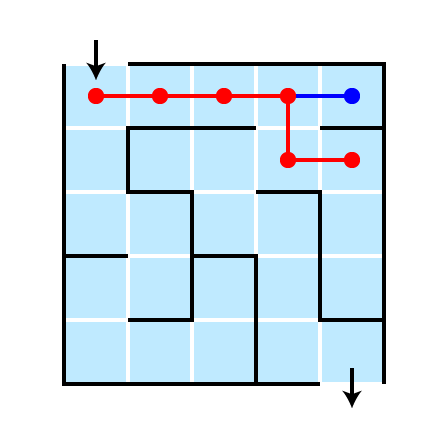
Two Stratgies
More Problems, Same Features
- Driving directions
- Solving puzzles
- Playing games
- tic-tac-toe
- chess
- …
- Tasks in artificial intelligence
Generic Problem
Input:
- Initial state
- Transition rules
- Goal state(s)
Output:
- Sequence of transitions from initial state to goal state
Example: Tower of Hanoi
- 3 pegs
- $n$ disks sit atop pegs
- move one peg at a time
- cannot place larger disk atop smaller
Initial State

Goal State
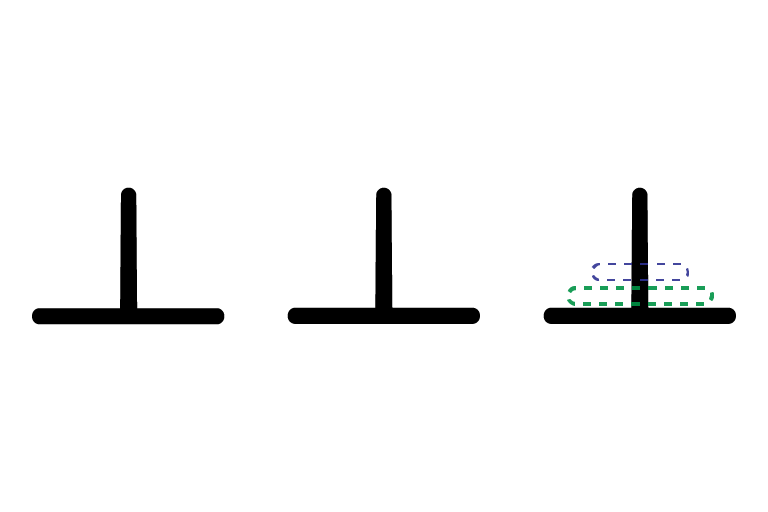
Transitions
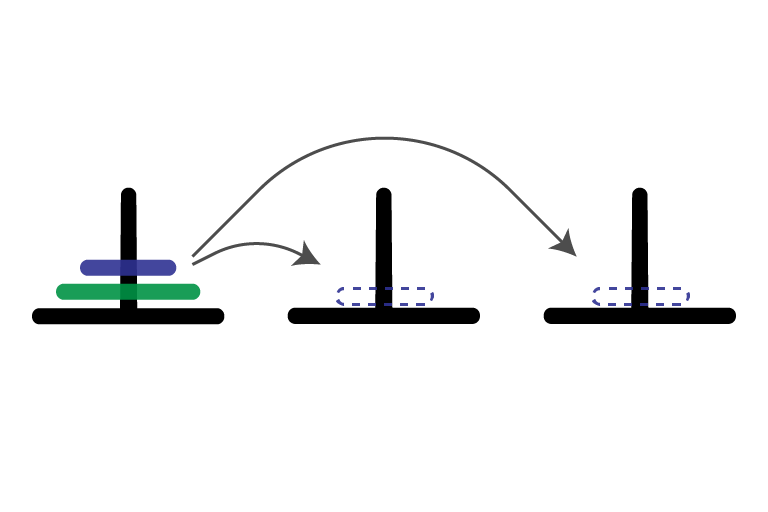
States and Transitions
- states are the configurations of the game
- collection of disks on each peg
- transitions connect one state to another if a single legal move transforms one to the other
State Diagram
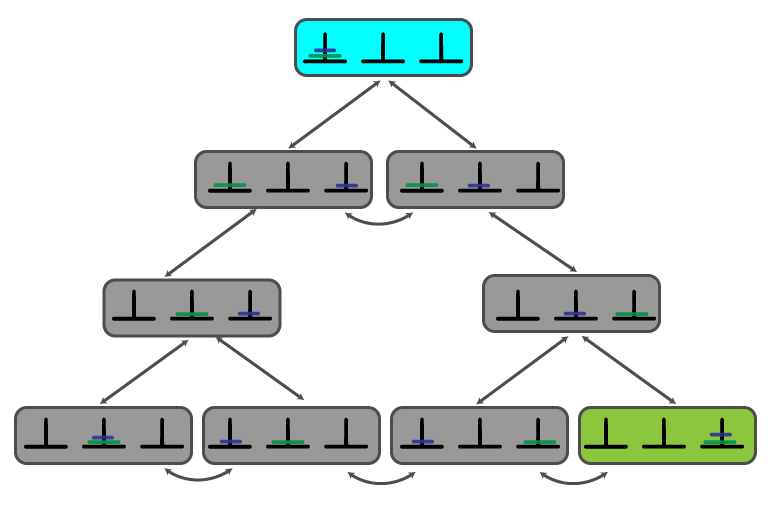
Solving ToH
- can use same strategy as maze solutions
- start at start state (blue above)
- search entire state space for goal state (green above)
- use DFS or BFS
- return path from start to goal state
What to Implement?
- class representing states
- method for computing neighbors of a state
- method for determining if a state is a goal
Abstract State Representation
abstract class State {
private State parent = null;
public abstract ArrayList<State> getNeighbors ();
public State getParent() { return parent; }
public void setParent(State parent) { this.parent = parent; }
public abstract boolean isGoal ();
}
Abstract Solution
- Use same strategies as maze
- breadth-first search (BFS)
- depth-first search (DFS)
- Same idea can be applied to any problem that can be encoded as:
- states and transitions
- given initial state
- want to find goal state
- Can write generic solver program
- solves problems without referencing which problem is being solved!
Generic DFS Solution
private static boolean getDFSolution (Stack<State> active, ArrayList<State> visited) {
if (active.peek().isGoal())
return true;
State cur = active.peek();
ArrayList<State> neighbors = cur.getNeighbors();
for (State s : neighbors) {
if (!visited.contains(s)) {
visited.add(s);
active.push(s);
if (getDFSolution(active, visited))
return true;
}
}
active.pop();
return false;
}
Generic BFS Solution
private static State getBFSolution (State start) {
ArrayList<State> visited = new ArrayList<State>();
Queue<State> active = new Queue<State>();
State next = start;
visited.add(next);
while (!next.isGoal()) {
for (State s : next.getNeighbors()) {
if (!visited.contains(s)) {
visited.add(s);
active.enqueue(s);
s.setParent(next);
}
}
if (!active.isEmpty())
next = active.dequeue();
else
return null;
}
return next;
}
State Space Search
- generic technique for solving loads of problems
- driving directions, puzzles, games, artificial intelligence,…
- can solve a problem without really knowing how!
How did we get here?
- represent input/states as interacting objects: object oriented design
- solve problems generically (polymorphism, interfaces, generic classes)
- same code can be used to solve many different problems
- store/access/manipulate states in data structures (arrays, linked lists)
- implement abstract data types (stacks, queues)
- generate solution to problems recursively (DFS)
Next Semester
COSC 211: Data Structures
- Deep dive into how to effectively store, organize, access, and manipulate data
- Rigorously reason about:
- correctness
- efficiency