Lecture 24: More Mazes

Last Time

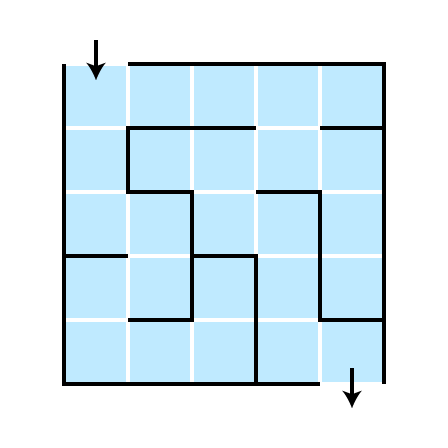
How Can We Solve Mazes?

Suggested strategy:

• Store visited cells
• Pick a direction, and go until dead end
  • walled in, or have already visited neighbors
• Backtrack until you see an unvisited neighboring node
• Continue in new direction

This strategy is depth-first

• Go as far as possible and backtrack

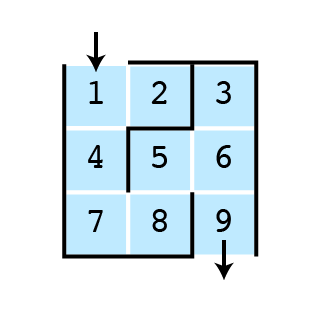
Strategy Illustrated

In More Detail

• fix an order on possible neighbors of cells
  • e.g., right, down, left, up
• when visiting a cell:
  • mark it as visited
  • check if it is the goal
  • if not, visit “next” unvisited neighbor
  • if no unvisited neighbors, return to “parent” cell

Representing a Maze in Code

• Cell class stores (among other things)
  • list of references to neighboring Cells (those not separated by walls)
• Maze class stores
  • 2d array of Cells
  • start and goal cells

How to Implement Solution?

• Store visited cells (How?)
• Store active cells (How?)
  • not yet exhausted
  • forms path back to start

Implementing Our Solution Strategy

• use an ArrayList to keep track of visited cells
• use a stack to keep track of active cells
  • active cells form a path from start to current cell
  • when we visit a new cell, push it to the stack
  • when we’ve explored all neighbors (and haven’t found the goal):
    • pop current cell off stack
    • return to previous cell on stack—cell from which we initially visited current cell

Illustration

Recursion: Our Old Friend

Use a stack an find goal recursively

• write method boolean solve (Stack<Cell> active, ArrayList<Cell> visited) {...}

How?

Stack-based solution

• idea: try to find goal from current cell (top of active)
  • if current is goal, return true
  • otherwise, find goal from unvisited neighbors:
    • push neighbor onto active stack and add neighbor to visited
    • call solve to continue exploration from new neighbor
  • if recursive call to solve returns true, we should return true too
  • if exploration fails to find anything pop current off stack and return false

When goal is found, active will contain the path from start to goal

Solution in Code

Question

Some of our solutions were really inefficient!

• goal could be adjacent to start, but a much longer path from start to goal is found

How could we ensure that we find the shortest path from start to goal?

Another Strategy

Explore in all directions simultaneously!

• Consider all possible first steps
• Then all possible second steps
  • ignore previously visited cells
• …

This strategy is breadth first

• Explore all possible next steps

Illustration: Depth 1

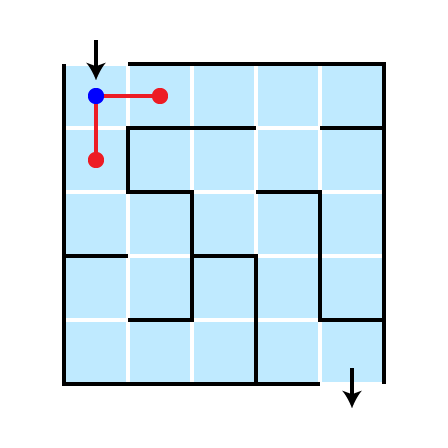
Illustration: Depth 2

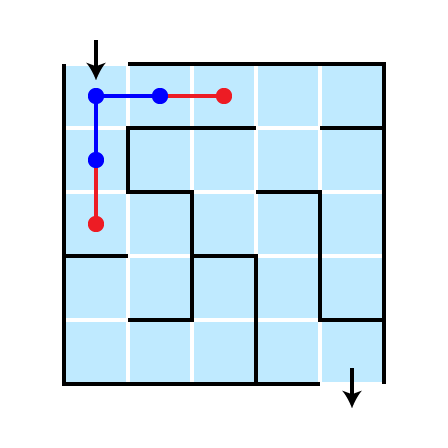
Illustration: Depth 3

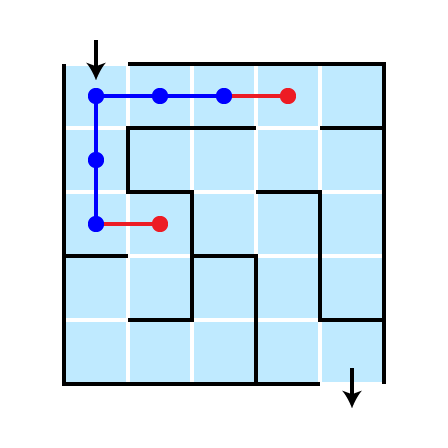
Illustration: Depth 4

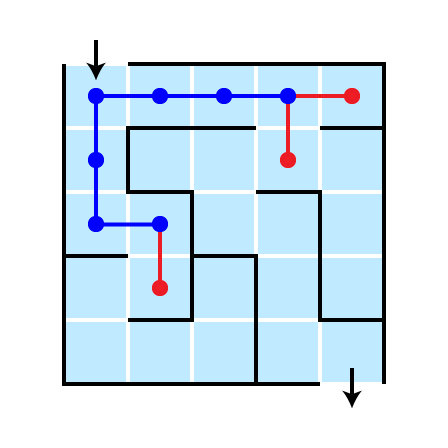
Completed Search

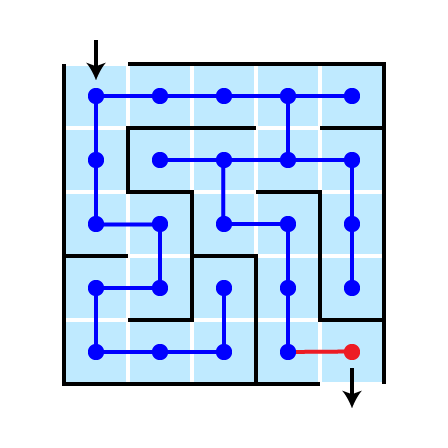
Return Solution

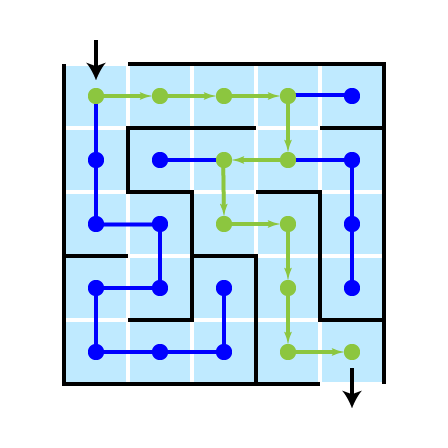
A Nice Feature

The shortest path from start to goal is found

• why?

Implementation Notes

• again, store visited and active
• active cells are boundary between visited and unvisited
• store active cells in a queue
  • all cells at distance $d$ from start are visited before any cell at distance $d+1$ is visited
• initially, active and visited are just starting cell
• each cell stores its parent cell
  • parent is cell from which cell was visited

Breadth-first Illustration

Breadth-first in Code

Two Solution Philosophies

1. Depth-first
   • Keep going until you can’t go any farther, then backtrack
   • Naturally suited to stack ADT
   • Naturally suited to recursive solution
2. Breadth-first
   • Exhaustively search all cells in increasing