Lecture 23: Josephus and Mazes

Overview

1. Josephus Problem
2. Solving Mazes

Last Time

1. Queue ADT
   • enqueue/dequeue operations
   • FIFO (first-in, first-out)
2. Josephus Problem

Josephus’ Manicure Problem

• $n$ people determine to give each other manicures
• they only have 1 set of tools/supplies
  • only one person can give another a manicure at a time
• once a person receives a manicure, they leave

Setup:

• people seated at a round table
• labeled sequentially clock-wise from $1$ to $n$

A System

• the current manicurist gives a manicure to the person seated to their left
• after the manicure, person to their left leaves
• the manicurist hands the tools to the next person to their left who becomes the next manicurist
• repeat until all but one person receives a manicure

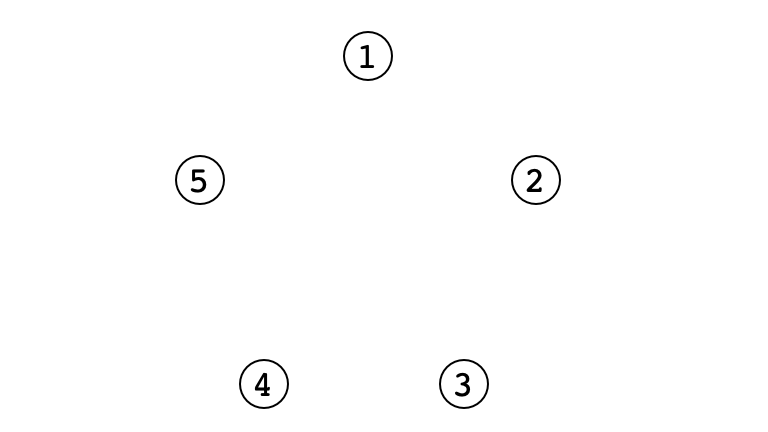
Initially, person 1 is manicurist.

Example $n = 5$

An Activity

• Devise a procedure for determining where Josephus should sit to avoid a manicure

• Use a queue!

  • assume your queue has a getSize() method

How Can We Find Josephus’ Spot?

Proposed Queue Solution

1. Add people 1 through n to a queue in order
   • head of queue is manicurist
   • person behind them receives manicure
2. Repeat until queue has size 1:
   1. dequeue manicurist
   2. enqueue manicurist
   3. dequeue receiver of manicure

Code Up a Solution!

Mazes

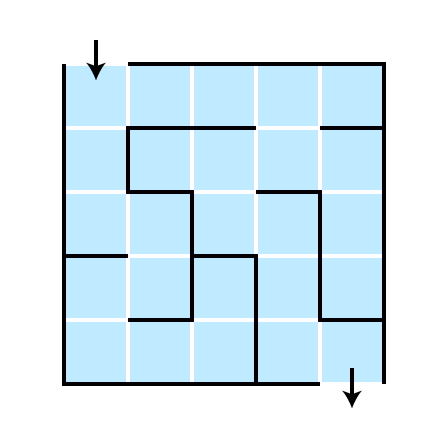
What is a Maze?

• a grid of cells
• each cell has up to 4 neighboring cells
  • some adjacent cells blocked off by walls
• specified starting cell and goal cell

Objective find a path from starting cell to goal cell

Maze Example

An Activity

How can we solve mazes in general?

• Come up with a procedure that will always find a solution to a maze
• No code

Maze Example