Lecture 22: Queues

Overview

1. The Queue Abstract Data Type
2. Linked List Queue Implementation
3. The Josephus Problem

Previously

Data Stuctures

• Arrays
• Linked Lists

Abstract Data Types

• Collection
  • add, remove, test for containment
• Stack
  • push, pop, peek

Stack Ordering

Stacks are Last In, First Out (LIFO):

• the last item pushed is next item popped

Often items should be processed in the order they arrive:

• First In, First Out (FIFO)

Examples:

• Standing in line
  • first come, first serve
• Communication buffers
  • reading from InputStream in, in.get() reads characters in order

The Queue

Another abstract data type: the queue

Supports two basic operations:

• void enq(T item) enqueue (add) an item to the end of the queue
• T deq() dequeue (remove) item from the front queue and return it

The first item enqueued is the first to be dequeued, etc

Visualizing Enqueue

Enqueue Another

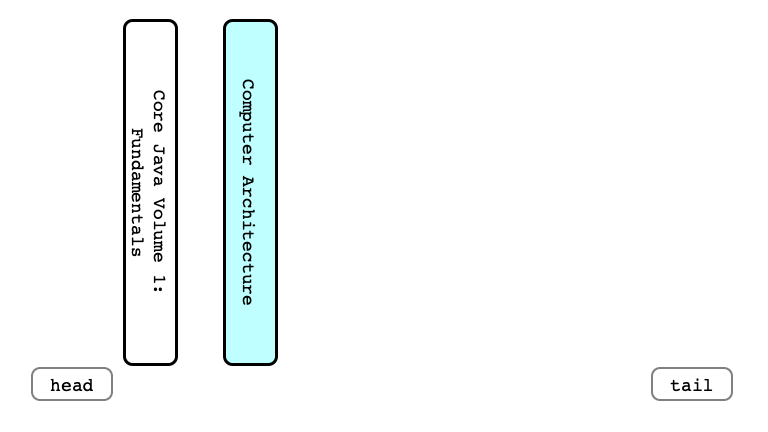
And Another

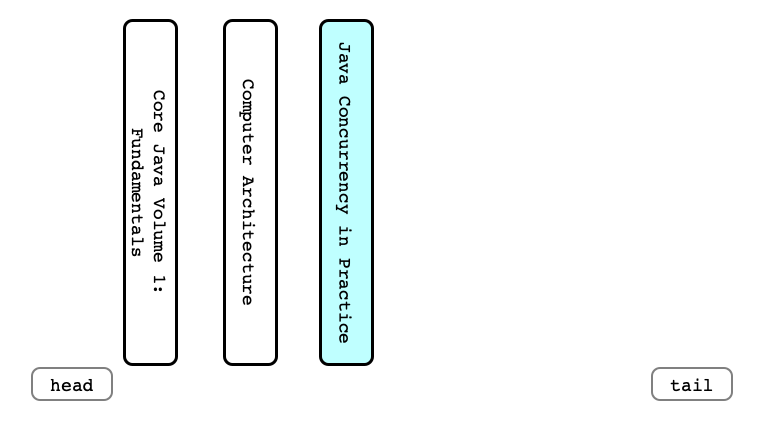
Dequeue Once

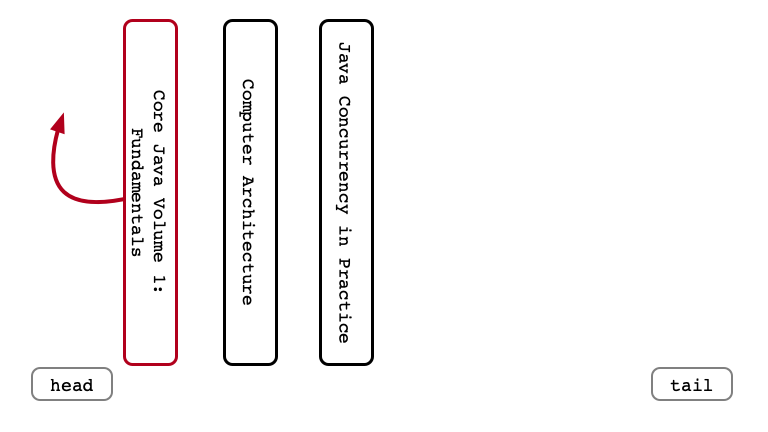
Enqueue Again

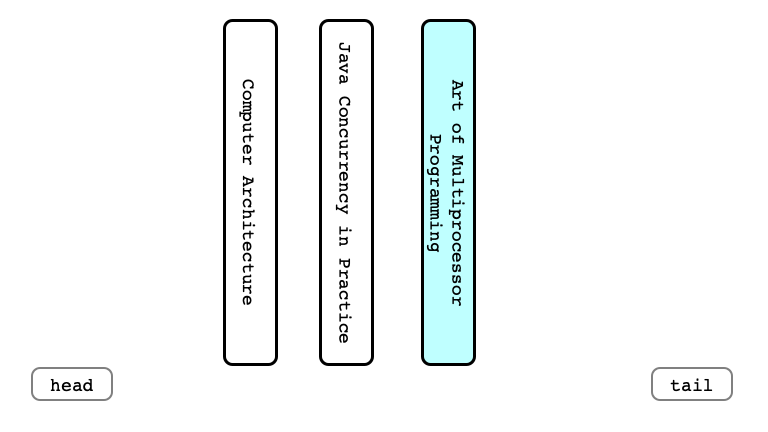
Dequeue Again

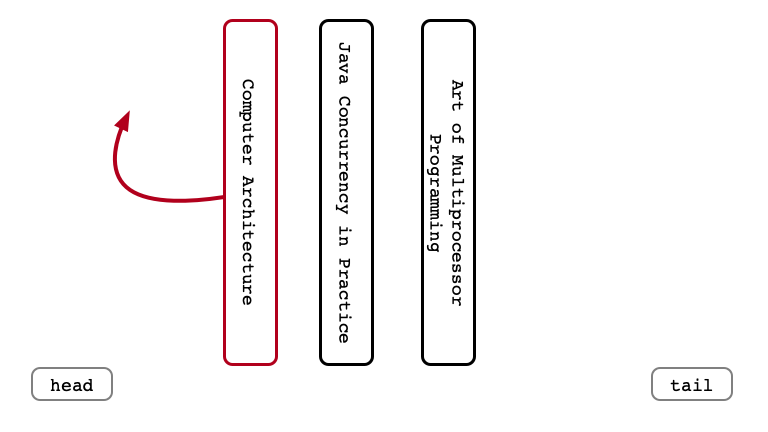
Enqueue Last Time

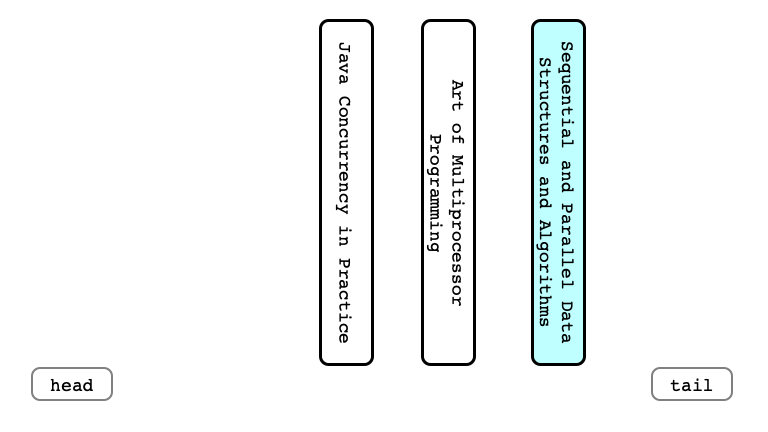
Implementing a Queue

How could we implement a queue with a linked list?

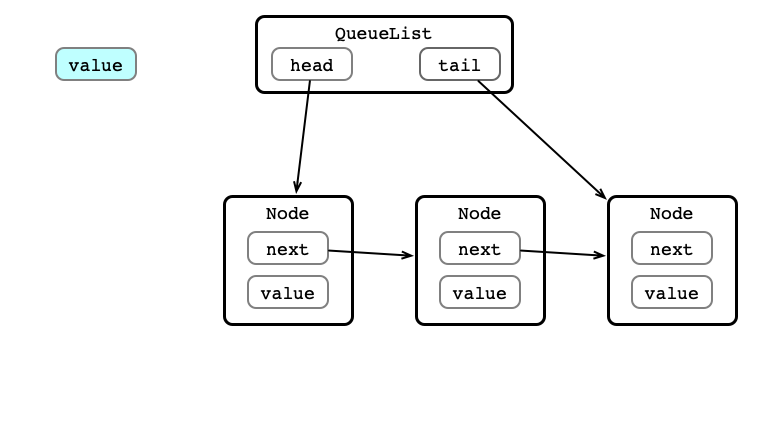
A QueueList

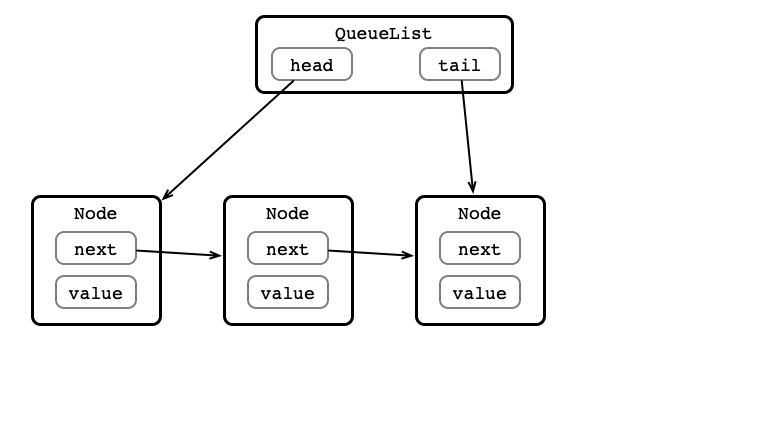
Enqueue Step 1

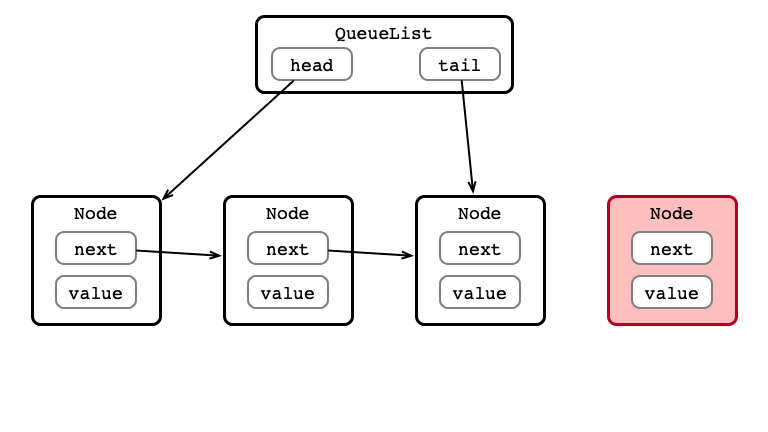
Enqueue Step 2

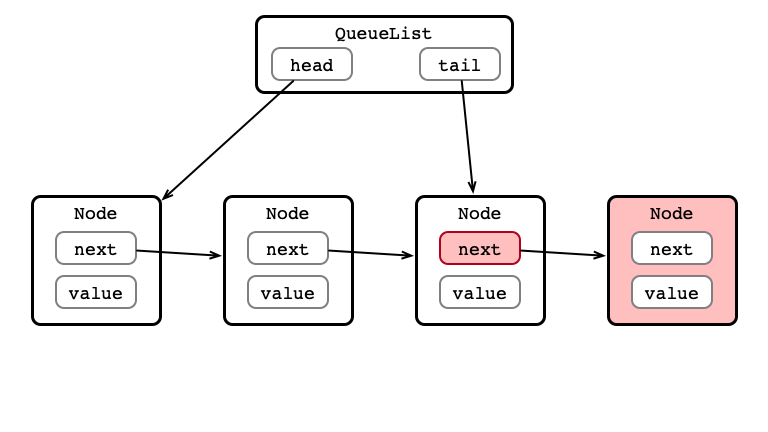
Enqueue Step 3

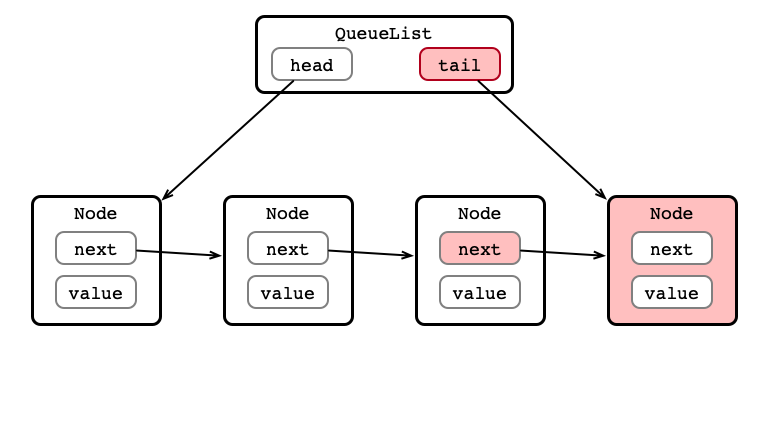
Item Enqueued! Dequeue?

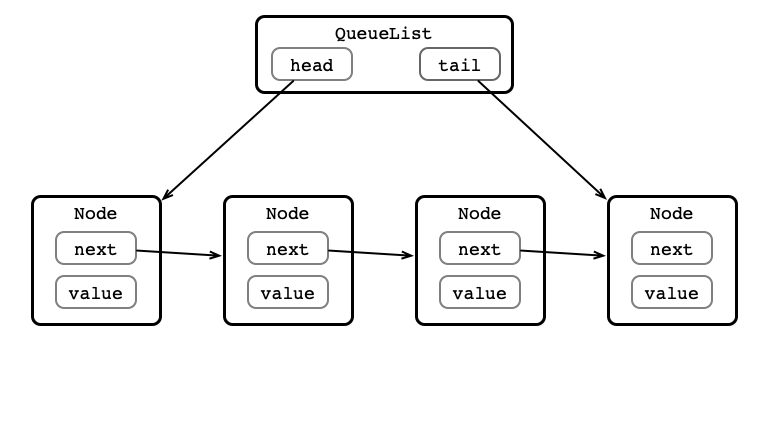
Dequeue Step 1

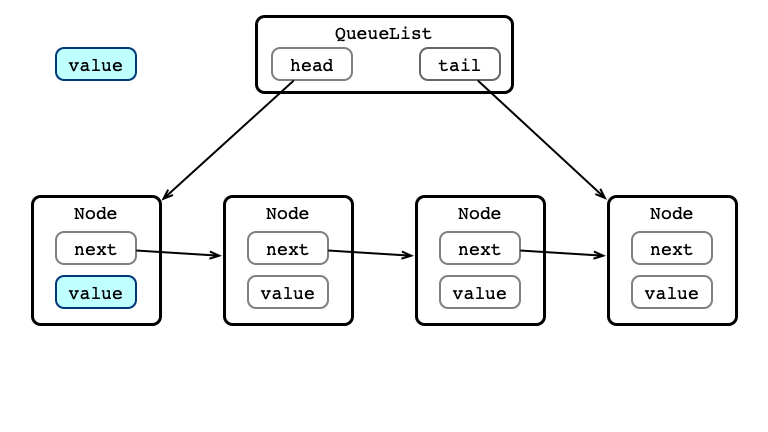
Dequeue Step 2

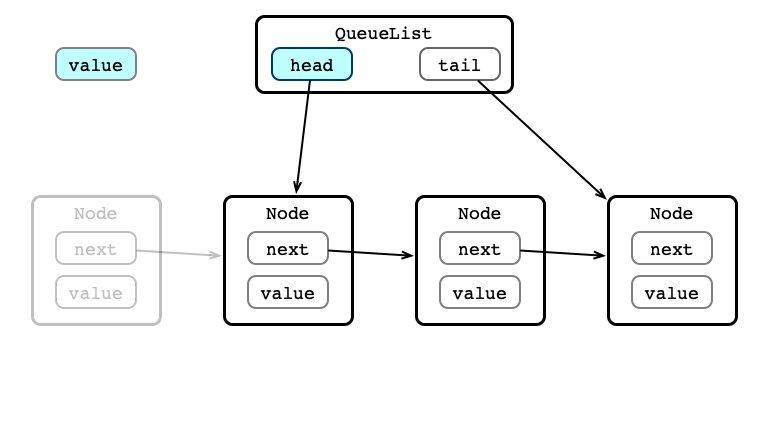
Dequeue Step 3

A Queue Interface

public interface SimpleQueue<T> {

    // Enqueue item to the queue
    void enq(T item);

    //Dequeue (i.e., remove and return) the first item in the queue. Returns null if the queue is currently empty
    T deq();
 
    // Determine if the queue is currently empty
    boolean isEmpty();
}

A Queue Implementation

public class QueueList<T> implements SimpleQueue<T>, Iterable<T> {
    private Node head = null;
    private Node tail = null;

    @Override
    public void enq(T item) {	
	Node nd = new Node(item);

	if (head == null) {
	    head = nd;
	    tail = nd;
	    return;
	}
	
	tail.next = nd;
	tail = nd;
    }

    @Override
    public T deq() {
	if (head == null) {
	    return null;
	}

	T item = head.item;
	head = head.next;
	return item;
    }

    @Override
    public boolean isEmpty() {
	return (head == null);
    }

    public T peek() {
	if (head == null) {
	    return null;
	}

	return head.item;
    }

    class Node {
	private Node next;
	private T item;

	public Node(T item) {
	    this.item = item;
	}
    }

    public Iterator<T> iterator() {
	return new ListIterator();
    }
    

    class ListIterator implements Iterator<T> {
	Node curr;
	
	public ListIterator() {
	    curr = head;
	}

	public boolean hasNext() {
	    return (curr != null);
	}

	public T next() {
	    if (curr == null) {
		return null;
	    }
	    
	    T item = curr.item;
	    curr = curr.next;
	    return item;
	}
    }
    
	
}

Testing the Queue

The Josephus Problem

• Historical problem inspired by Josephus’ The Jewish War
• We will consider a less gruesome retelling of the problem

Josephus’ Manicure Problem

• $n$ people determine to give each other manicures
• they only have 1 set of tools/supplies
  • only one person can give another a manicure at a time
• once a person receives a manicure, they leave

Setup:

• people seated at a round table
• labeled sequentially clock-wise from $1$ to $n$

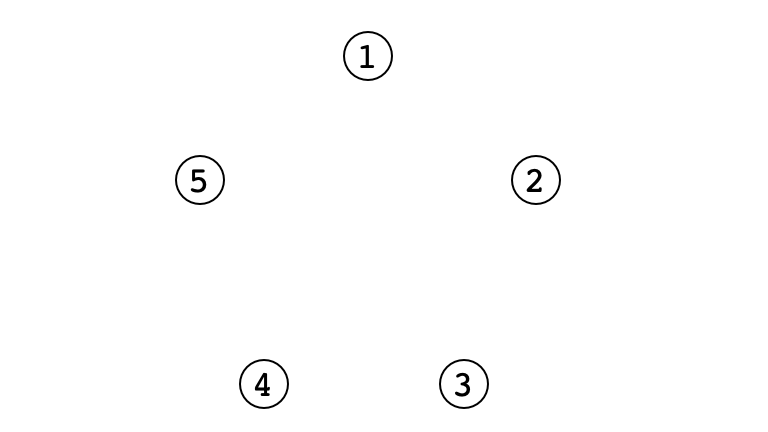
Illustration $n = 5$

A System

• the current manicurist gives a manicure to the person seated to their left
• after the manicure, person to their left leaves
• the manicurist hands the tools to the next person to their left who becomes the next manicurist
• repeat until all but one person receives a manicure

Initially, person 1 is manicurist.

Example $n = 5$

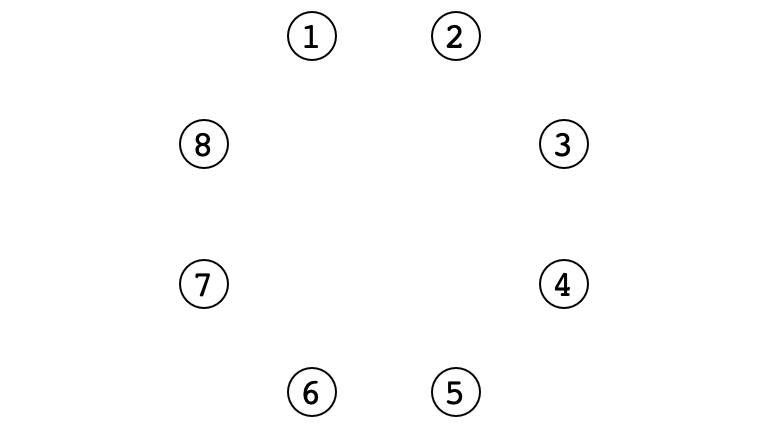
Example $n = 8$

A Wrinkle

Josephus does not want a manicure!

Question. Where should Josephus sit at the table to ensure that he does not receive a manicure?

An Activity

• Devise a procedure for determining where Josephus should sit to avoid a manicure

• Use a queue!

  • assume your queue has a getSize() method

How Can We Find Josephus’ Spot?

How Can We Code a Solution?