Lecture 21: Stacks and Balanced Expressions

Overview

1. Project 3: Stable Matchings
2. Balanced Expressions
3. Queues

Project 3: Stable Matchings

Stable Marriage Problem

Setup:

• 2 sets of agents
  • residents
  • hospitals
• want to match residents to hospitals
  • each resident assigned to one hospital
  • each hospital assigned one resident
• agents have preferences
  • residents rank hospitals
  • hospitals rank residents

How should we match hospitals and residents?

Background

Problem formalized by Gale & Shapley, 1962

• Defined a criterion for a “good” matching: stability
• Described an algorithm to find a stable matching

Central problem in economics

• 1,000’s of academic articles
  • including several by me
• 4+ books devoted solely to this problem
• 2012 Nobel Prize in Economics (Shapley & Roth)

And recently: Marriage Pact

Input

• A set $H$ of hospitals
• A set $R$ of residents
• For each hospital $h$:
  • a ranked list of all residents
• For each resident $r$
  • a ranked list of all hospitals

Example:

    hospitals
    A B
    residents
    a b
    preferences
    a: A B
    b: A B
    A: a b
    B: a b

Output

    hospitals
    A B
    residents
    a b
    preferences
    a: A B
    b: A B
    A: a b
    B: a b

Goal: find a matching where no hospital-resident pair has an incentive to deviate

Blocking Pairs

    hospitals
    A B
    residents
    a b
    preferences
    a: A B
    b: A B
    A: a b
    B: a b

Consider matching (a, B), (b, A)

The pair (a, A) is a blocking pair.

Stability

A matching without blocking pairs is stable.

    hospitals
    A B
    residents
    a b
    preferences
    a: A B
    b: A B
    A: a b
    B: a b

Consider matching (a, A), (b, B)

An Algorithm (McVitie & Wilson)

1. Residents arrive one at a time
2. When a resident arrives, proposes to first choice hospital
3. When a hospital receives a proposal:
   • if no other proposals yet, provisially accept
   • otherwise compare proposals
     • provisionally accept preferred proposal
     • refuse less preferred proposal
4. When a resident receives refusal
   • propose to next choice hospital

Continue until all residents arrive

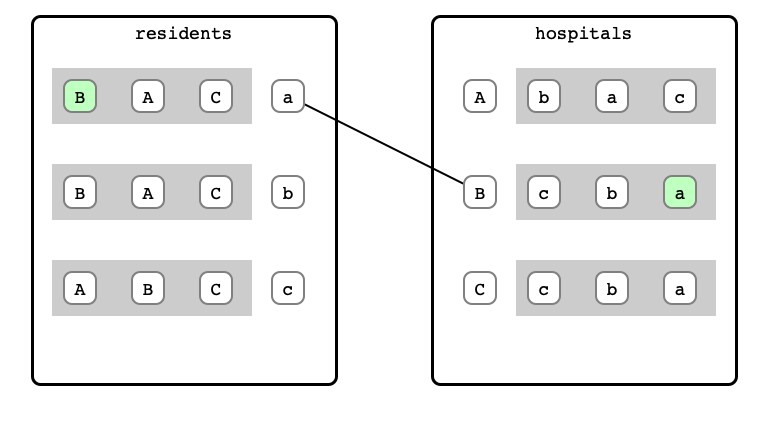
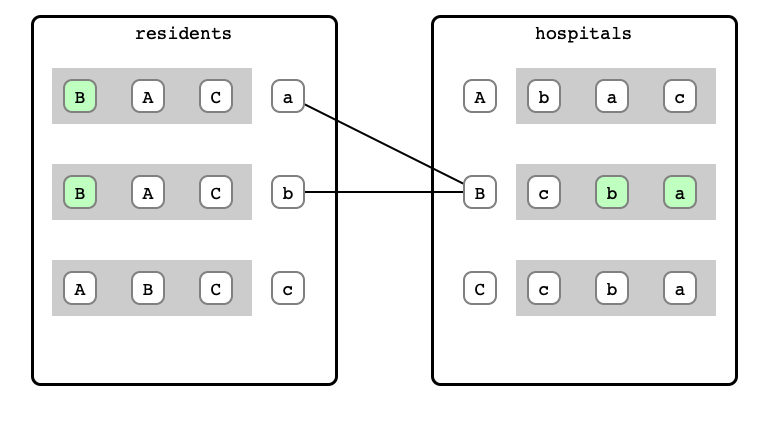
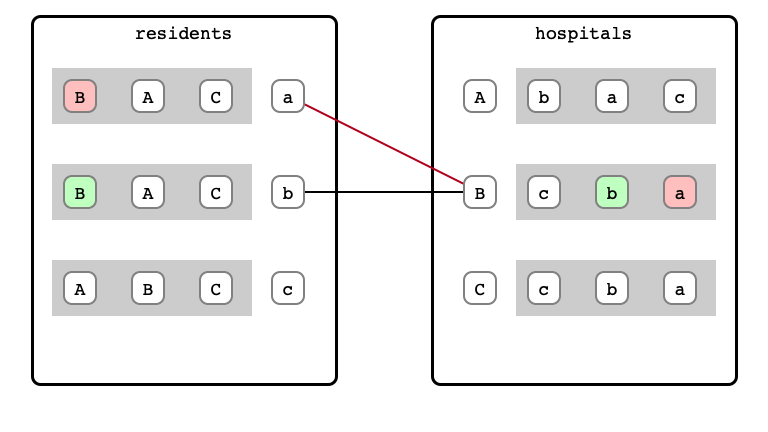
Algorithm Example

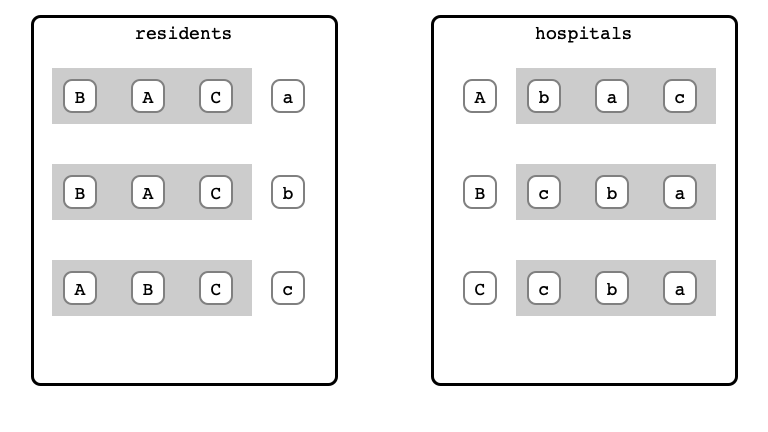
M & W Step 1: a proposal

M & W Step 2: b proposal

M & W Step 3: B refusal

M & W Step 4: a proposal

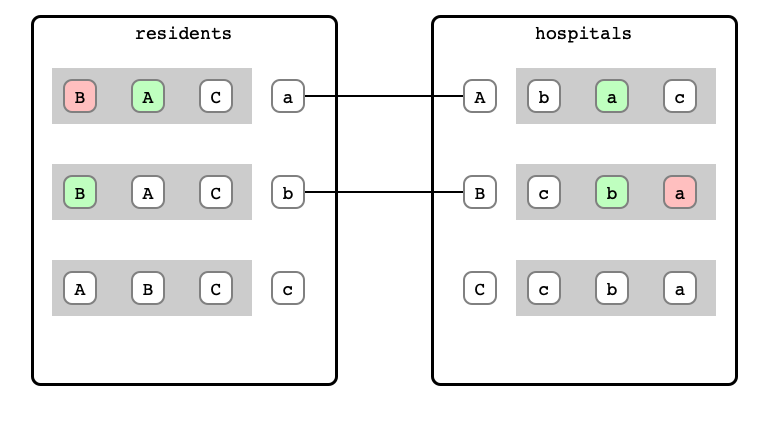
M & W Step 5: c proposal

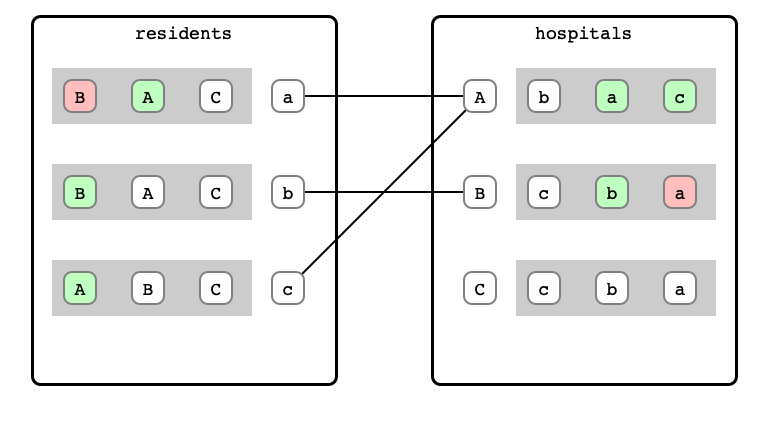
M & W Step 6: A refusal

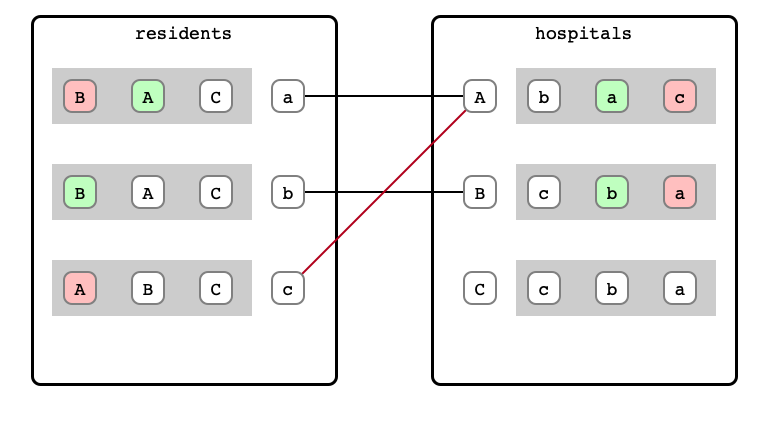
M & W Step 7: c proposal

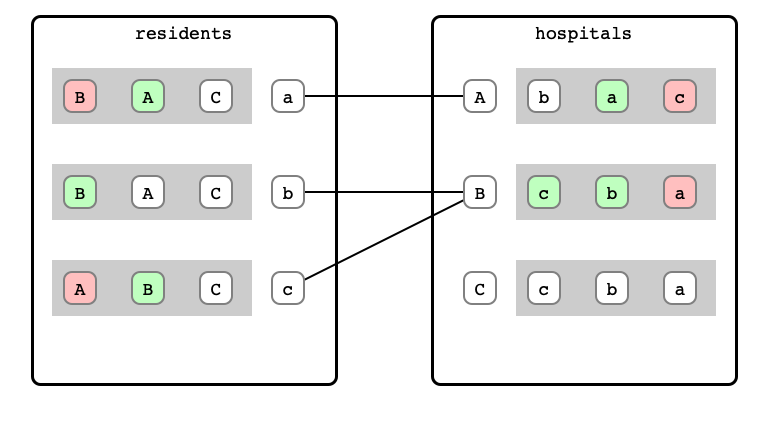
M & W Step 8: B refusal

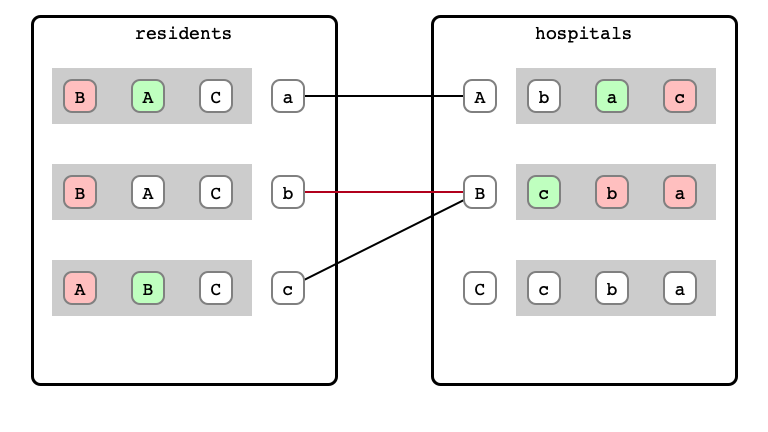
M & W Step 9: b proposal

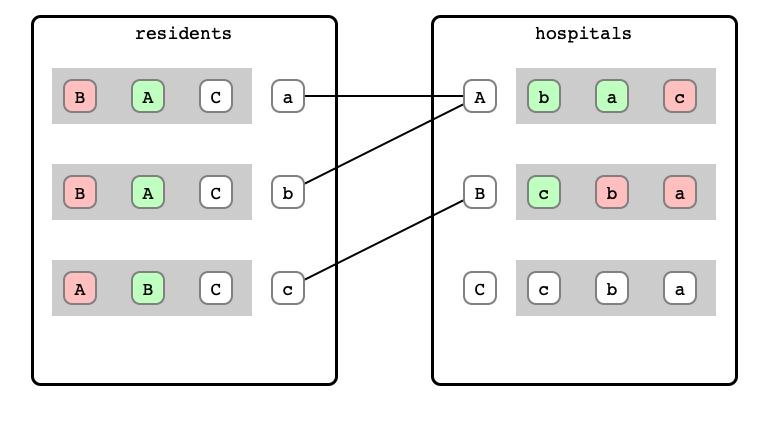
M & W Step 10: A refusal

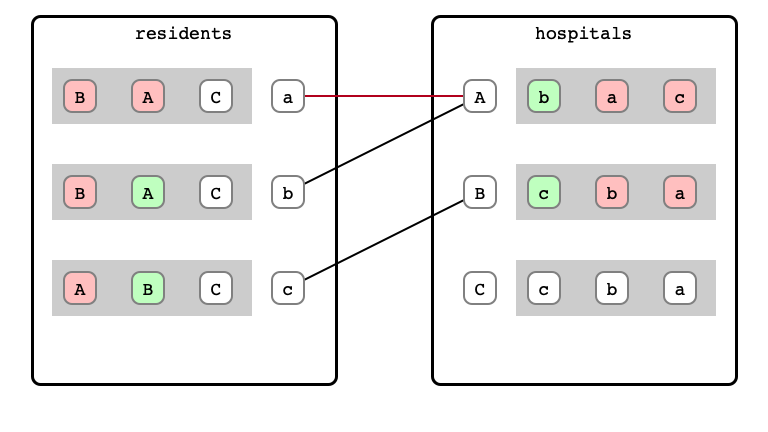
M & W Step 11: a proposal

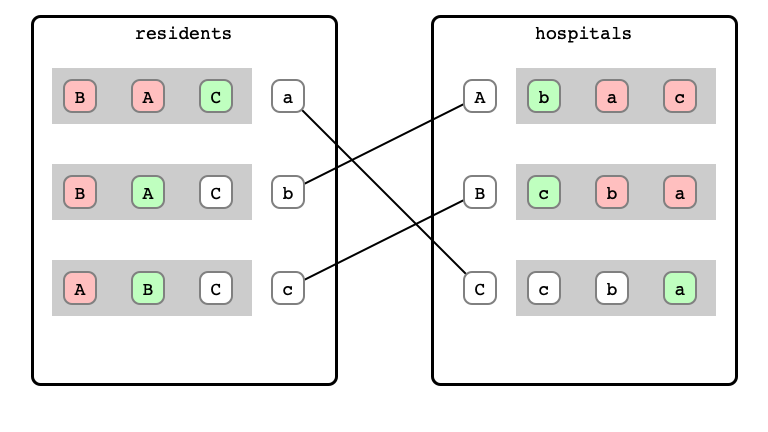
And Done!

Project 3

Implement McVitie & Wilson algorithm to find stable matchings!

• Provided with examples/tests

Balanced Expressions

Brackets

Java uses a lot of brackets:

• curly braces { ... }
• parentheses ( ... )
• square brackets [ ... ]

If expression are properly bracketed, Java compiler complains!

An Abstraction

This expression

public class HelloWorld {
    public static void main(String[] args)} {
        System.out.println("Hello, World!");
    }
}

but with just the brackets:

{ ( [ ] ) } { ( ) } }

Question

When is an expression properly bracketed?

• What makes { ( [ ] ) } { ( ) } } okay?
• What makes { ( [ ] ) } } { ( ) } } not?

Balanced Expressions

A bracketed expression is balanced if

1. every opening bracket has a corresponding closing bracket
   • closing bracket appears after opening bracket
   • one-to-one correspondence between opening and closing
2. opening-closing pairs are nested
   • if opening bracket appears between opening-closing pair, then corresponding closing bracket does too

{    {    {    }    }    {    }    {    }    }

{    {    }    }    }    {    }

How To Check For Balance?

{    {    {    }    }    {    }    {    }    }

Balance Checking with a Stack

1. Scan expression from left to right
2. Whenever an open bracket is encountered, push it to the stack
3. When a closing bracket is encountered:
   • check if it matches top of stack
   • if so, pop the stack
   • if not, or stack is empty, expression is not balanced!
4. If stack is not empty at end of expression, expression is not balanced!

Checking for Balance

{    {    {    }    }    {    }    {    }    }

Implementation