Lecture 04: Recursion III

Outline

1. Tower of Hanoi
   • recursive strategy
   • in code
2. Concluding Thoughts on Recursion
3. Preview: Defining New Objects

Last Time: Tower of Hanoi

Setup

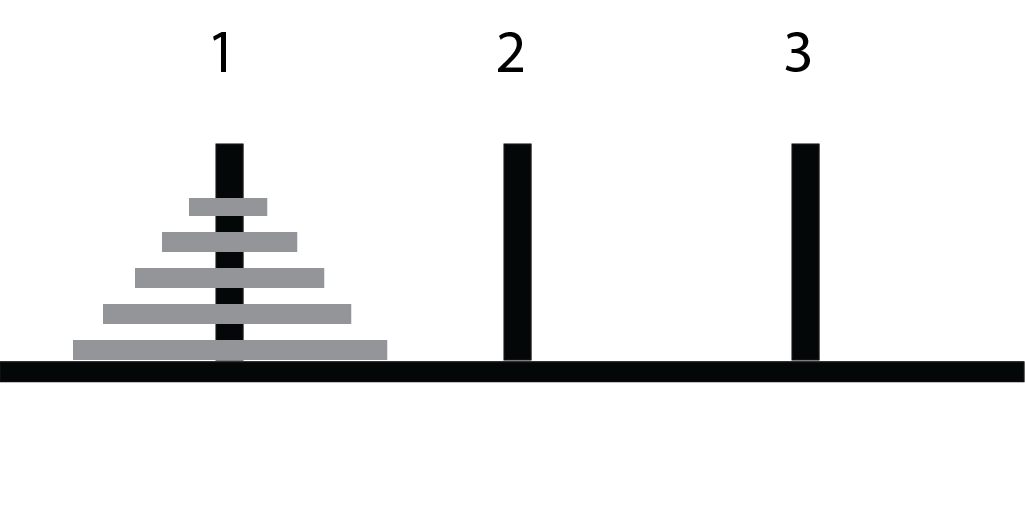
Goal

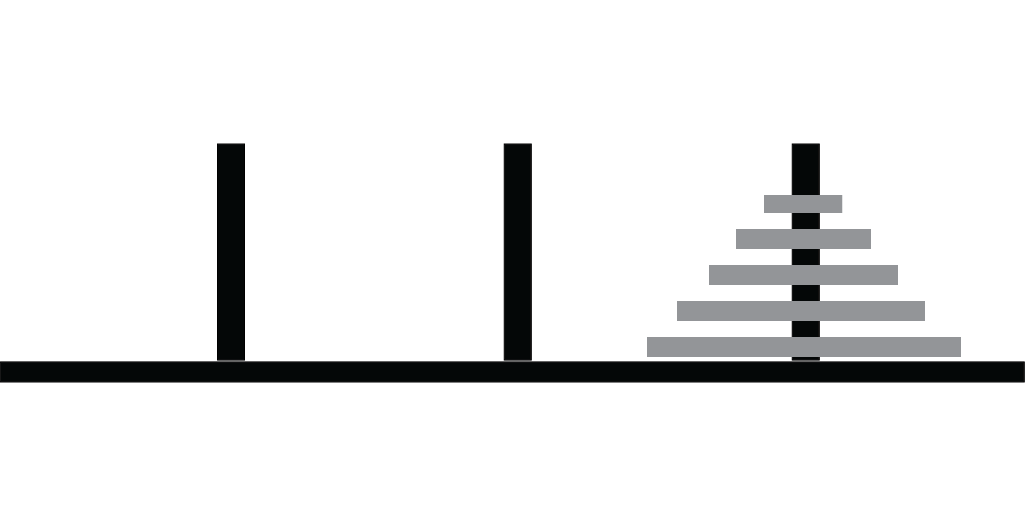
Rules

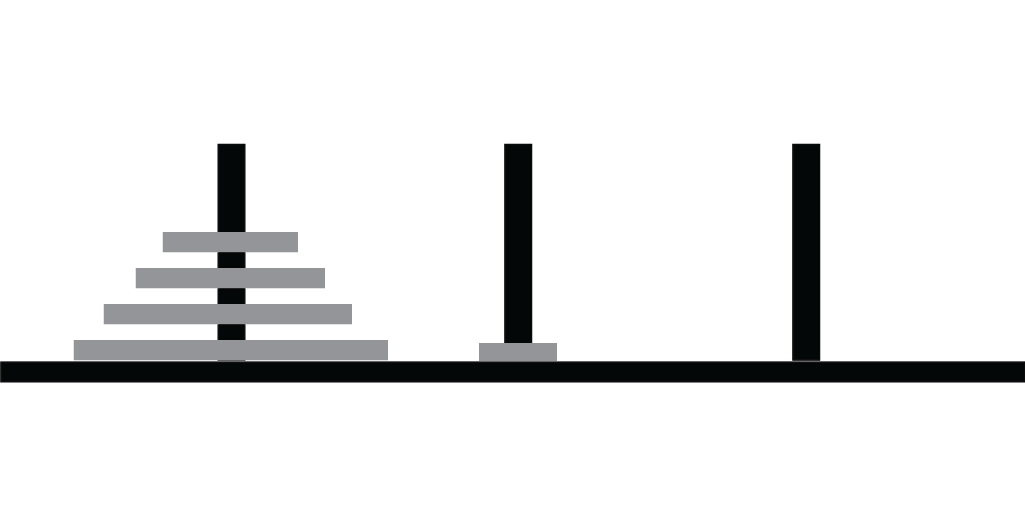
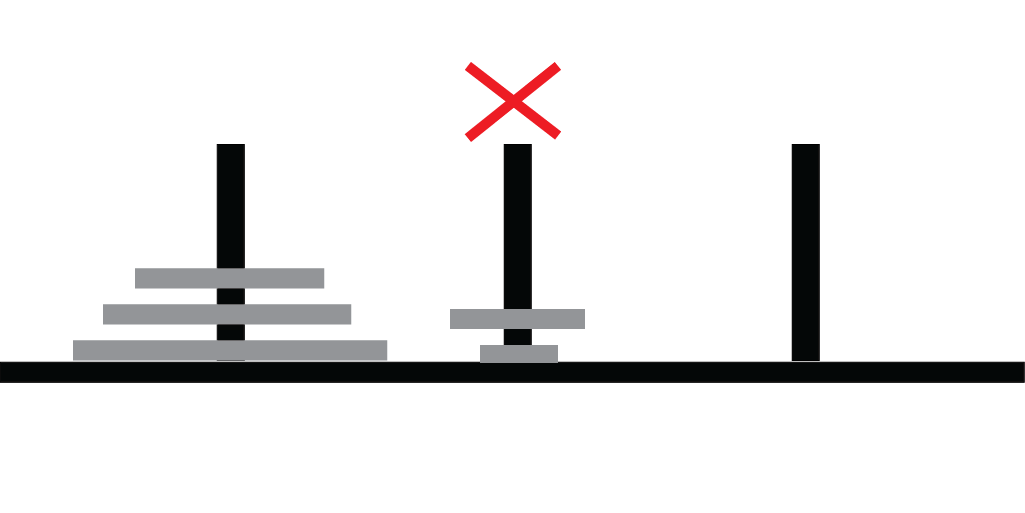
A Program

Want:

• A program that generates instructions for a solution
• Example solution for 2 disks

Move disk from peg 1 to peg 2
Move disk from peg 1 to peg 3
Move disk from peg 2 to peg 3

Solution for 3 Disks?

Moving the Largest Disk

How to move largest disk from peg 1 to peg 3?

Solving in 3 Steps (1)

Step 1: Move subtower to peg 2

Solving in 3 Steps (2)

Step 2: Move bottom disk to peg 3

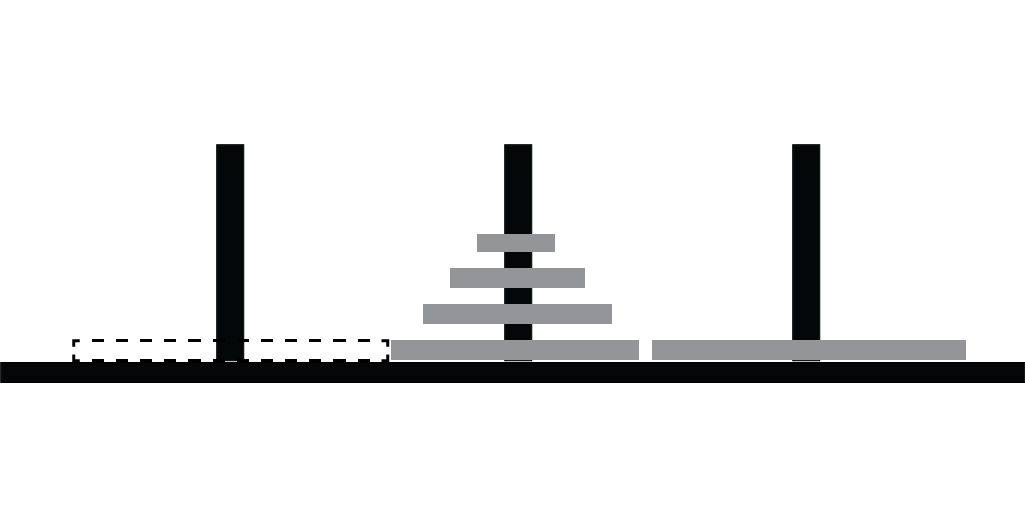
Solving in 3 Steps (3)

Step 3: Move subtower to peg 3

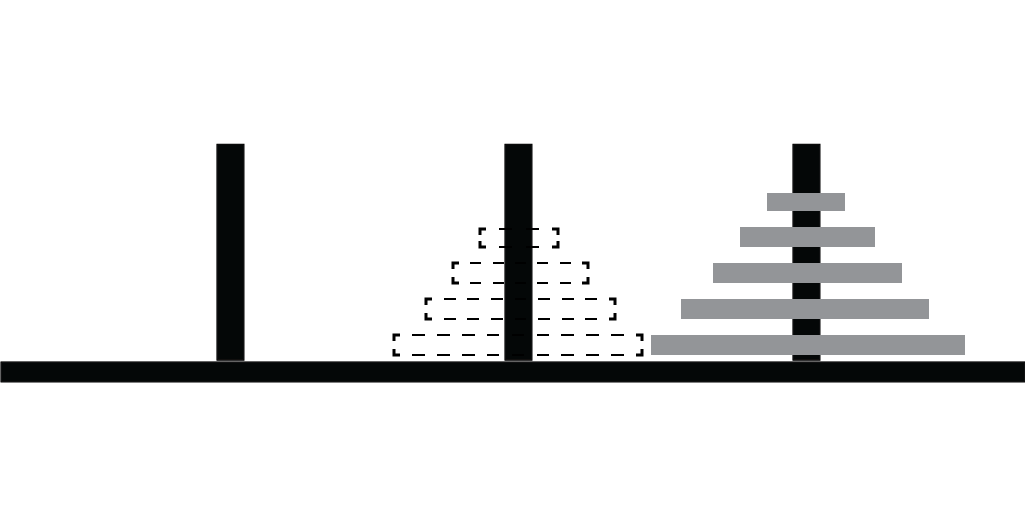
Moving a Sub-Tower

How do we move \(m\) disks from peg \(i\) to peg \(j\)?

A General Procedure

To move \(m\) disks from peg \(i\) to \(j\):

1. move \(m - 1\) disks from \(i\) to \(k\) (other peg)
2. move one disk from \(i\) to \(j\)
3. move \(m - 1\) disks from \(k\) to \(j\)

What is missing?

Base Case!

If \(m = 1\), just print

Move disk from peg i to peg j

Let’s try it in code!

TowerOfHanoi.java

How Efficient is our Solution?

void move (int m, int from, int to, int other) {
    if (m == 1) {
        System.out.println("Move disk from " + from + " to " + to);
        return;
    }
	
	move(m - 1, from, other, to);
	move(1, from, to, other);
	move(m - 1, other, to, from);		
}

Counting Recursive Calls

If \(f(m )\) is number of instructions printed to move \(m\) disks:

• \(f(m) = 2 \cdot f(m-1) + f(1)\), and \(f(1) = 1\)
• So we get:
  • $f(1) = 1$
  • $f(2) = 2 \cdot f(1) + 1 = 3$
  • $f(3) = 2 \cdot f(2) + 1 = 7$
  • $\vdots$
  • $f(m) = 2^m - 1$
• This is a lot of instructions!
  • $f(10) \approx 1,000$, $f(20) \approx 1,000,000$, $f(30) \approx 1,000,000,000$

But…

Solving Tower of Hanoi with $m$ disks requires $2^m - 1$ instructions!

• The solution generated by our program is optimal
• Requires only 5 lines of code!

Concluding Thoughts on Recursion

Factorial

private static int factorial(int n) {
    if (n == 1) return 1;
    return n * factorial(n - 1);
}

Fibonacci

private static int fibonacci (int n) {
    if (n <= 2) return 1;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

Tower of Hanoi

private static void move (int num, int from, int to, int other) {
    if (num == 1) {
        System.out.println("Move disk from " + from + " to " + to + "." );
        return;
    }
    move(num - 1, from, other, to);
    move(1, from, to, other);
    move(num - 1, other, to, from);
}

Evaluation

1. Factorial: simple code and efficient execution
2. Fibonacci: simple code, but inefficient execution
3. ToH: surprisingly simple; perhaps mysterious; large solution
   • but solution is still optimal

Moral

Recursion is…

• subtle
• sometimes efficient, sometimes not
• powerful
• miraculous
• confusing

How Confusing?

public static long collatz (long n) {
    if (n == 1) return 1;
    if (n % 2 == 0) return collatz (n / 2);
    else return collatz (3 * n + 1);
}

Insanity

public static long collatz (long n) {
    if (n == 1) return 1;
    if (n % 2 == 0) return collatz (n / 2);
    else return collatz (3 * n + 1);
}

• It is not known if this method has an infinite loop for some value of n
• This is not for lack of interest in the problem:
  • Worked on by some of the most celebrated mathematicians of the last century

Up Next: Defining New Objects