Lecture 03: Recursion II

Outline

1. Recap of Last Time
2. (In)efficiency of Recursion
3. Magic of Recursion

Last Time

1. Looked at recursive methods for factorial and Fibonacci numbers
2. Compared iterative and recursive solutions for Fibonacci

Factorial Solutions

Iterative:

    private static long iFactorial (long n) {
	    if (n <= 1) { return 1; }

        long val = 1;
        for (long i = 2; i <= n; i++) {
            val *= i;
        }
	    
        return val;
    }

Recursive:

    private static long rFactorial (long n) {
	    if (n <= 1) { return 1; }
	    return n * rFactorial(n - 1);
    }

Comparing the Solutions

Recursive is more succinct… but let’s test their performance!

• RecursiveFactorialTester.java

Fibonacci Solutions

Iterative:

    private static long iFib (long n) {
        long prev = 0; long cur = 1; long next;

        for (long count = 1; count < n; count++) {
            next = prev + cur;
            prev = cur;
            cur = next;
        }
		
        return cur;
    }

Recursive:

    private static long rFib (long n) {
        if (n <= 2) return 1;
		
        return rFib(n-1) + rFib(n-2);
    }

Comparing the Performance

• RecursiveFibonacciTester.java

What happened?

Why is this:

    private static long rFactorial (long n) {
	    if (n <= 1) { return 1; }
	    return n * rFactorial(n - 1);
    }

so much more efficient than this:

    private static long rFib (long n) {
        if (n <= 2) return 1;
		
        return rFib(n-1) + rFib(n-2);
    }

Factorial Recursive Calls

    private static long rFactorial (long n) {
	    if (n <= 1) { return 1; }
	    return n * rFactorial(n - 1);
    }

Fibonacci Recursive Calls

    private static long rFib (long n) {
        if (n <= 2) return 1;
		
        return rFib(n-1) + rFib(n-2);
    }

Some Observations

1. The iterative solutions were efficient.
2. Recursive factorials were efficient because no branching:
   • each method call made only one recursive call
3. Recursive Fibonacci was inefficient because of branching:
   • each method call made 2 recursive calls
   • even though few distinct calls, all method calls executed as prescribed by code

Magic

Previous Examples

• Extremely simple recursive methods
• Still simple iterative methods

Tower of Hanoi Puzzle

Recall the Tower of Hanoi Puzzle:

1. 3 pegs: 1, 2, 3
2. stack of \(n\) disks of decreasing size on first peg
3. can only move one peg at a time
4. cannot put larger disk on top of a smaller disk

Goal. Move all disks from peg 1 to peg 3

Initial Configuration

All disks on first peg

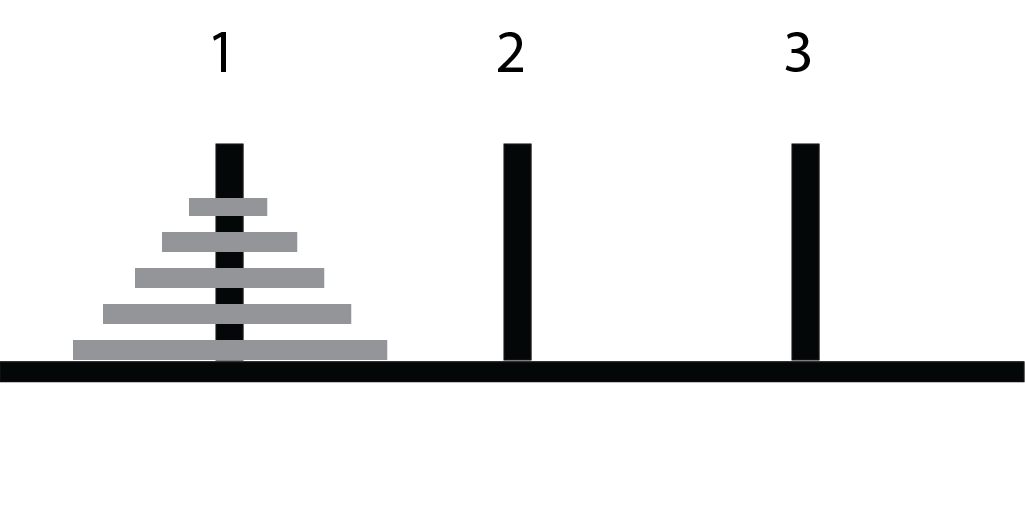
Rule 1

Move one disk at a time

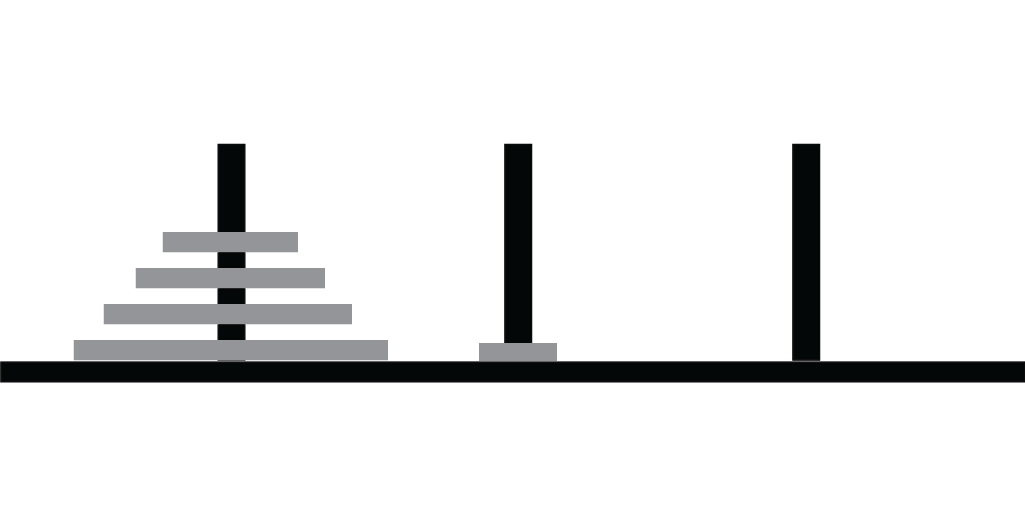
Rule 2

Cannot place a larger disk atop a smaller disk

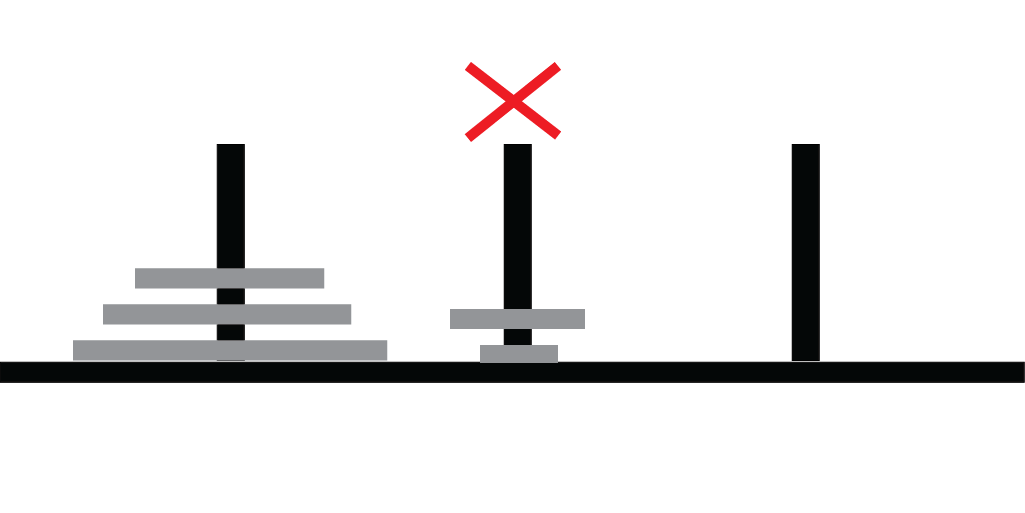
Goal

To move all disks from peg 1 to peg 3

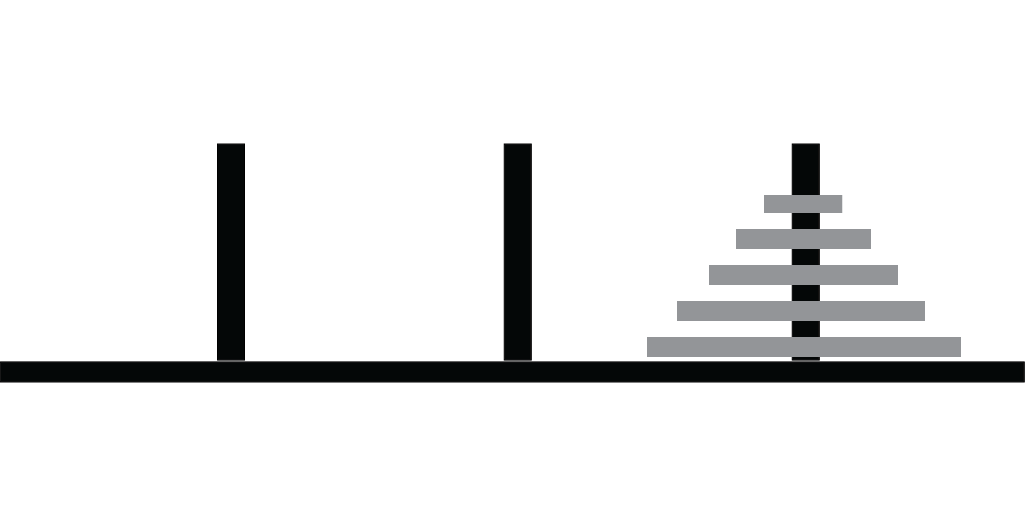
A Program

Want:

• A program that generates instructions for a solution
• Example solution for 2 disks

Move disk from peg 1 to peg 2
Move disk from peg 1 to peg 3
Move disk from peg 2 to peg 3

A Problem

How do we design the program?

Hints:

• Think recursion!
• What has to happen before largest disk can be moved?

Discuss!

• Worksheet link