Packet Forwarding with a Locally Bursty Adversary
Will Rosenbaum
Amherst College
A Simple Model
Simple Model for Packet Forwarding
Network
- network is a path of $n$ buffers
-
packets have common destination: rightmost node

Execution in synchronous rounds
- 1 packet injected per round (arbitrary buffer)
- each buffer can forward at most one packet per round
Goal. Deliver packets using minimum space per buffer
Previous Work
- For centralized protocols, buffer space 2 is necessary and sufficient
- Forward-if-empty protocol
- Miller & Patt-Shamir, DISC 2016
- For local protocols, buffer space $\Theta(\log n)$ is necessary and sufficient
- Odd-Even Downhill (OED) protocol
- Dobrev et al., SPAA 2017; Patt-Shamir & R– PODC 2017
- For protocols with locality $d$, buffer space $\Theta(1 + \frac 1 d \log n)$ is necessary and sufficient
- Patt-Shamir & R– INFOCOM 2019
Generalizing the Model: AQT
Adversarial Queueing Theory (Borodin et al. STOC 1996)
- rate $\rho$
- burst parameter $\sigma$
- edge capacity $C$
Executions
- in any $t$ consecutive rounds, adversary can inject $\rho t + \sigma$ packets
- each buffer can forward $C (\geq \rho)$ packets
Previous Results in AQT Model
-
For cenralized protocols, buffer space $2 \rho + \sigma$ is necessary and sufficient
-
For local protocols, buffer space $\Theta(\rho \log n + \sigma)$ is necessary and sufficient (?)
-
For protocols with locality $d$, buffer space $\Theta(1 + \frac \rho d \log n + \sigma)$ is necessary and sufficient
- ugly algorithm/analysis for $C > 1$
Local Bursts: Refining the AQT Model
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
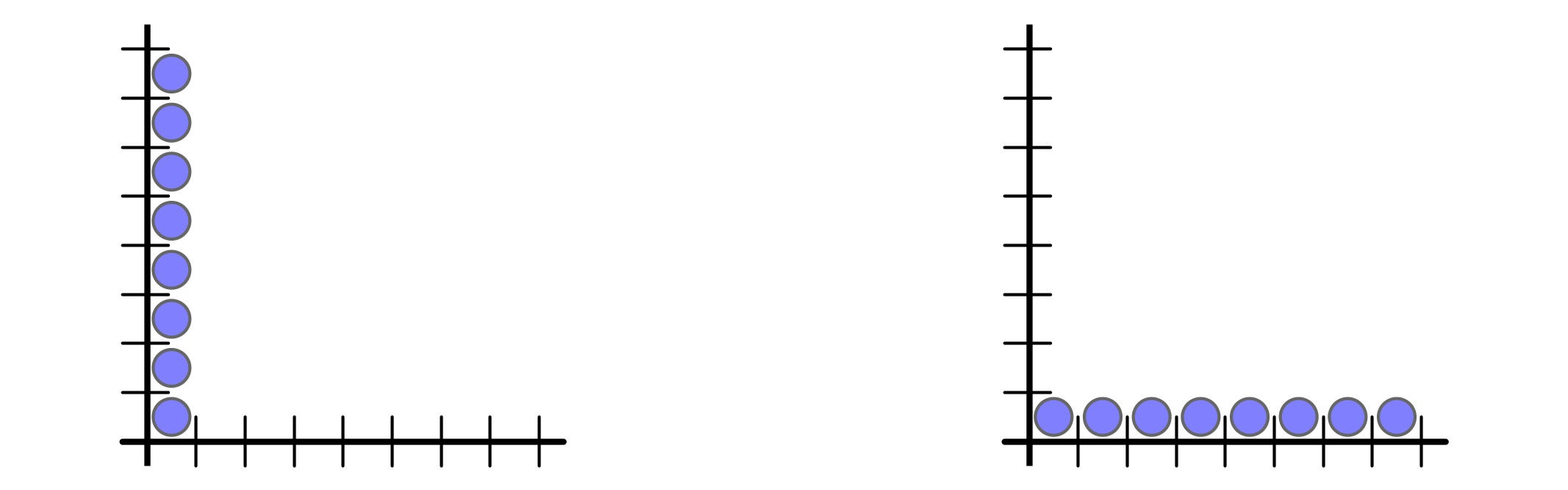
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
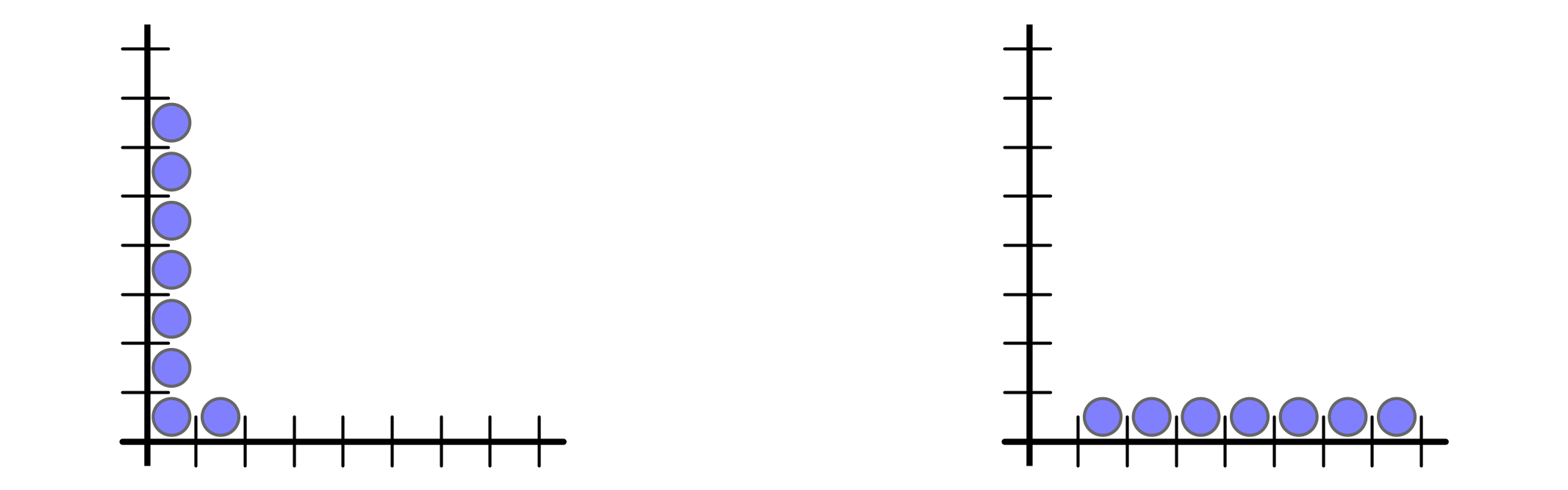
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
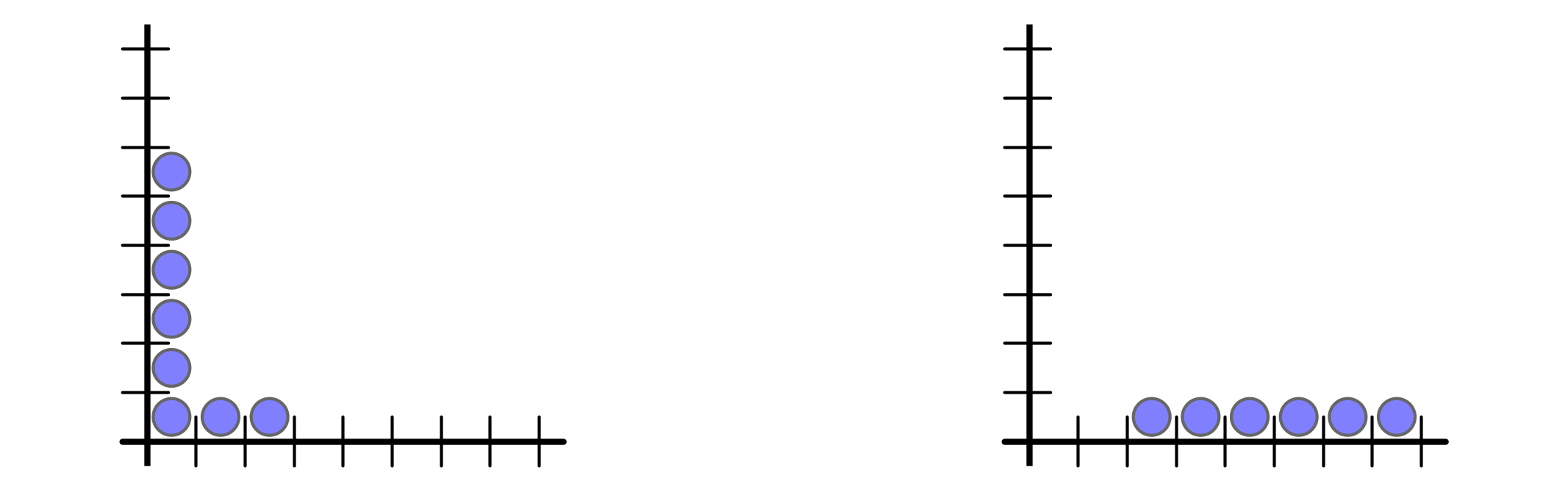
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
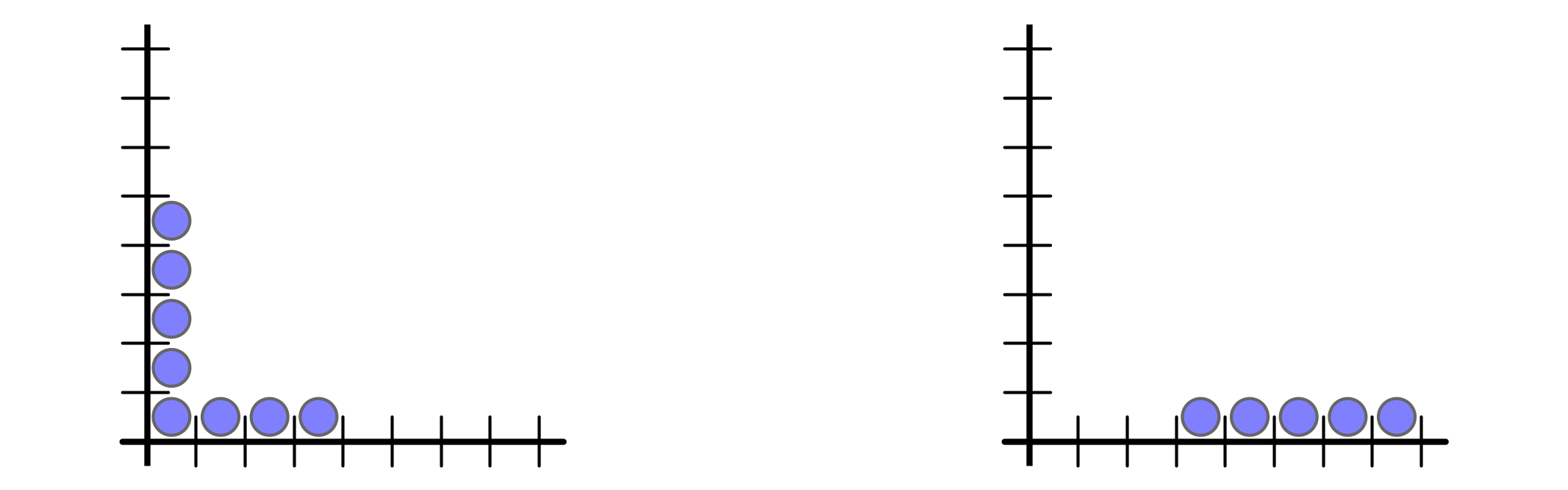
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
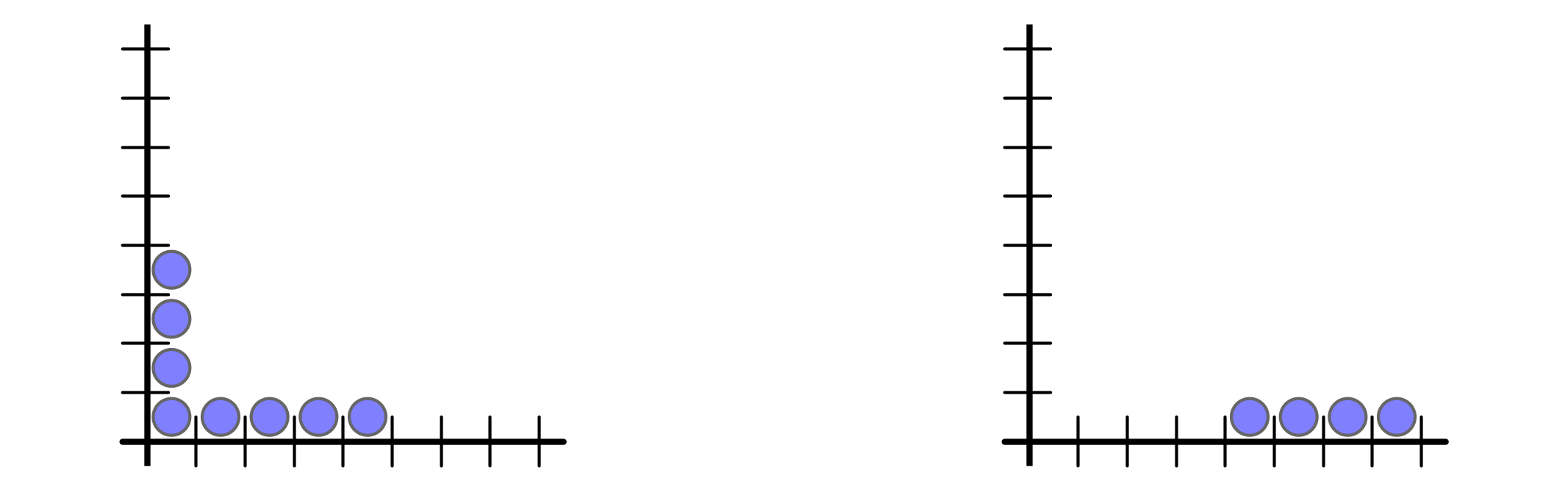
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
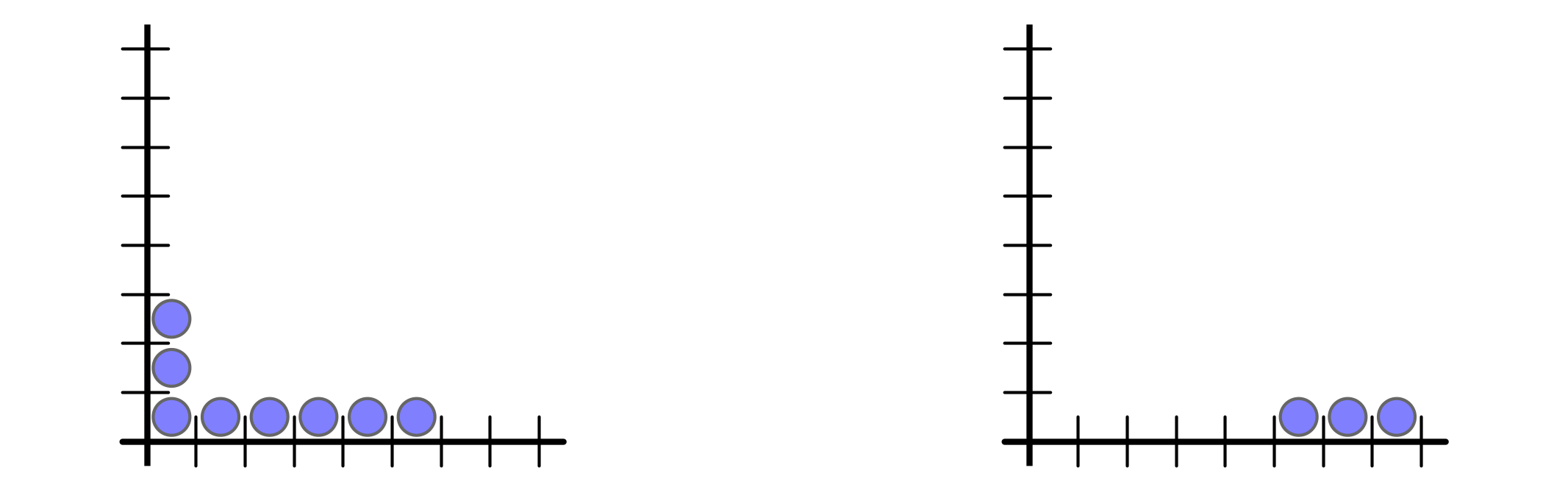
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
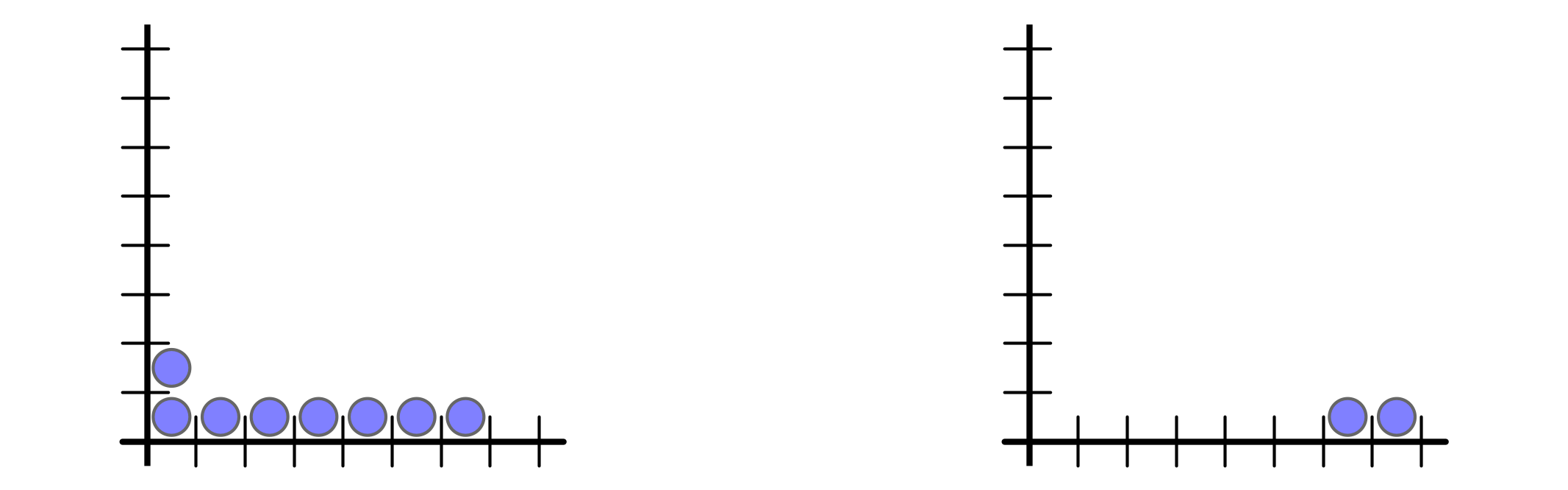
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
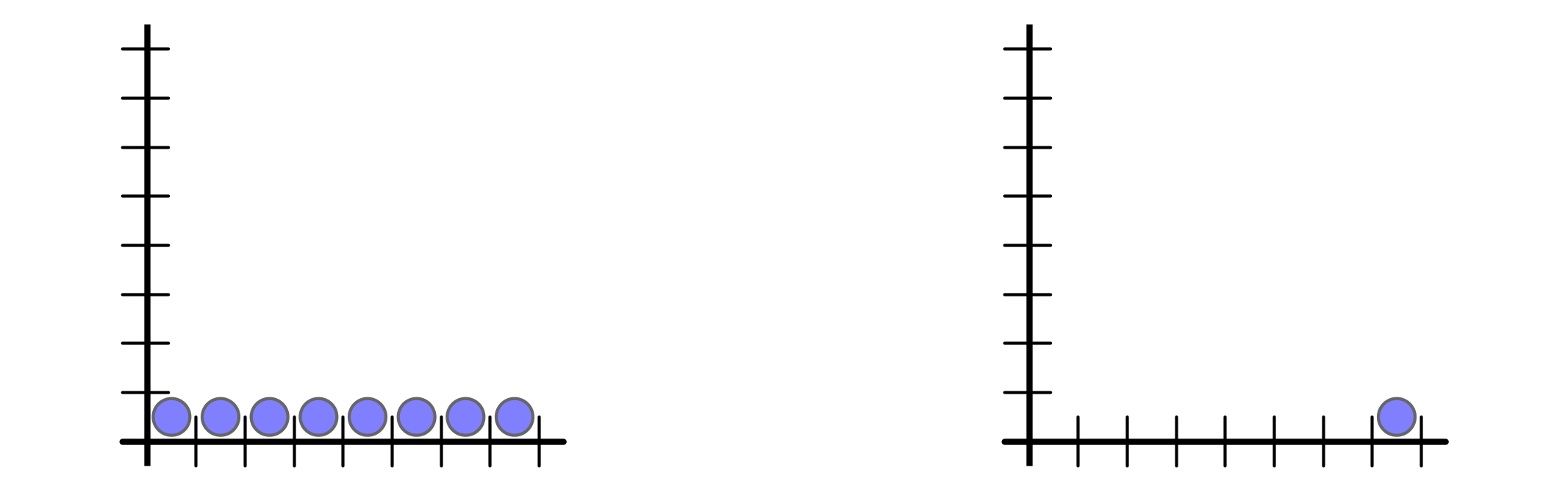
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
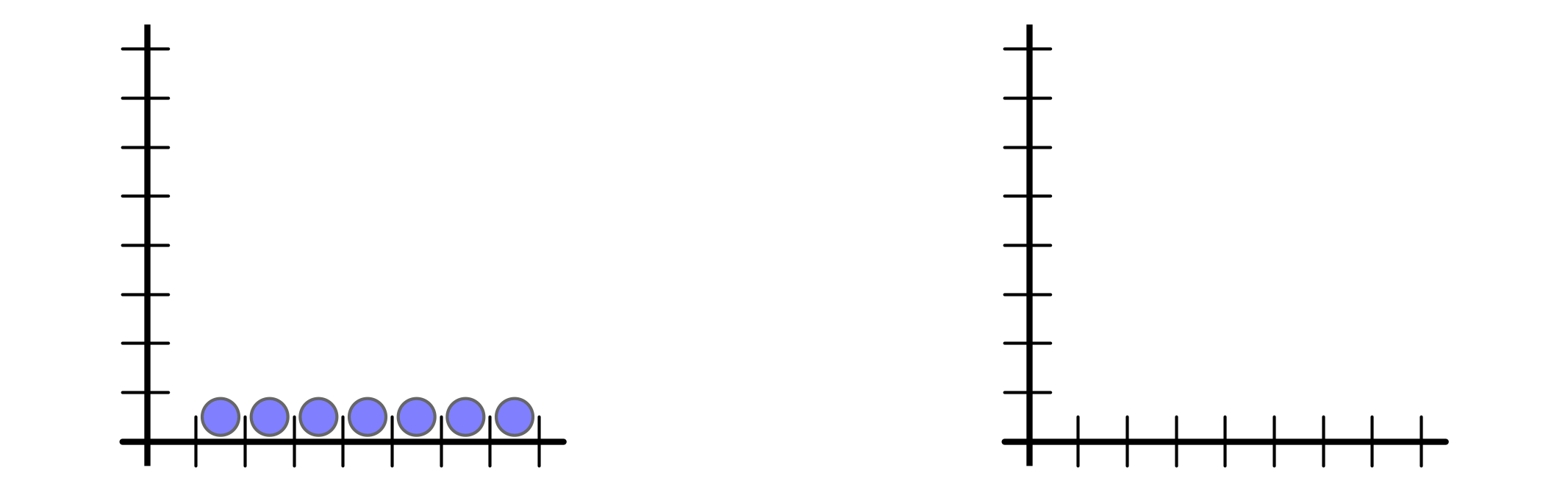
But buffer space requirement is $n$ vs $1$
Global Bursts
AQT parameters do not distinguish ($\rho = 1, \sigma = n - 1$):
-
Ex 1 every $n$ rounds, inject $n$ packets into buffer $1$
-
Ex 2 every $n$ rounds, injection $1$ packet into buffers $1, 2, \ldots, n$
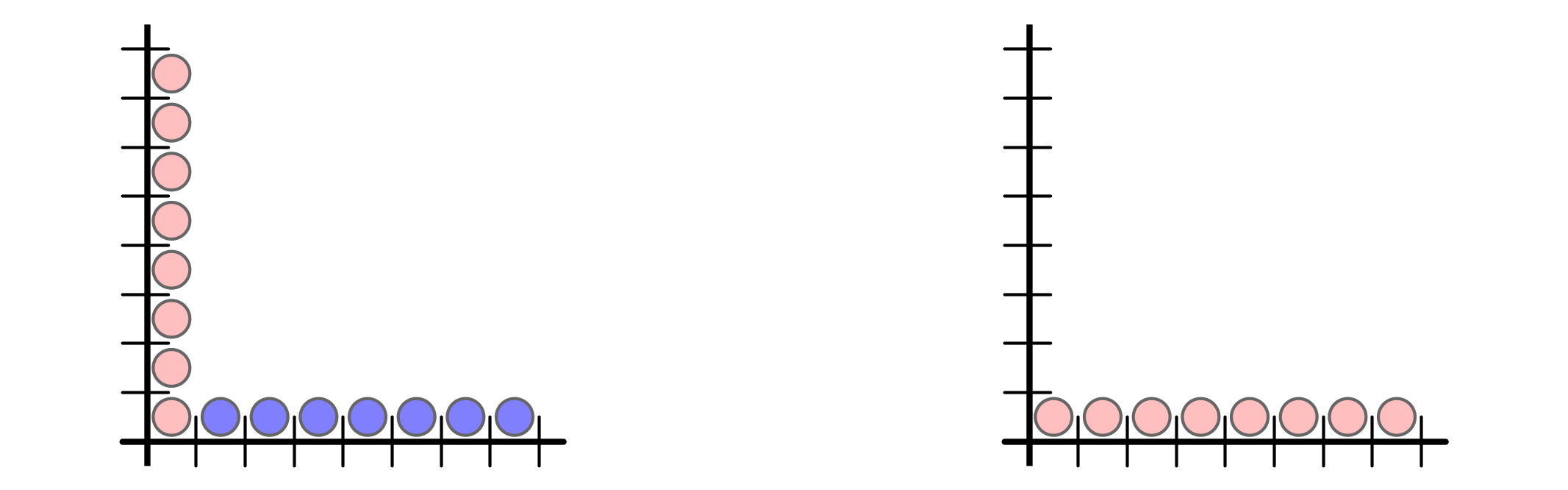
But buffer space requirement is $n$ vs $1$
Proposed Model
Locally Bursty Adversaries (LBAs)
- distinguish packets by origin
- local burst parameter $B$
- for every set $S$ of buffers, $t$ consecutive rounds
- number of packets injected into $S$ is at most $B \vert S \vert + \rho t$
Previous examples
- Ex 1 has local burst parameter $B = n - 1$
- Ex 2 has local burst parameter $B = 1$
LBA is strict refinement of AQT model
Packet Bundling and LBAs
Issue with Previous Protocol Analyses
General capacities, $C$
- simple protocols defined for $C = 1$
- reasoning about $C > 1$ is subtle
- how many packets should each buffer forward?
- how to deal with “fractional part” of load?
- previous OED analysis was incomplete!
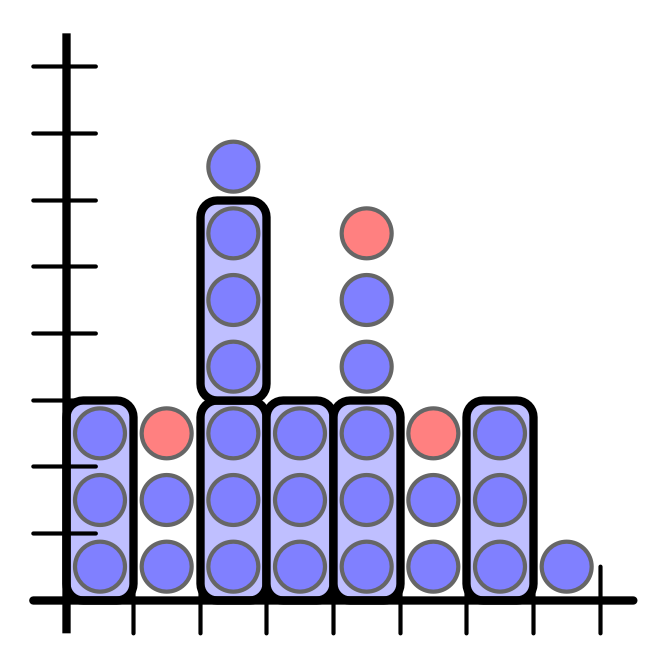
Packet Bundling Strategy, $C > 1$
- bundle groups of $C$ packets together
- treat bundles as individual packets
- ignore fractional part
-
apply protocol for $C = 1$ to bundles
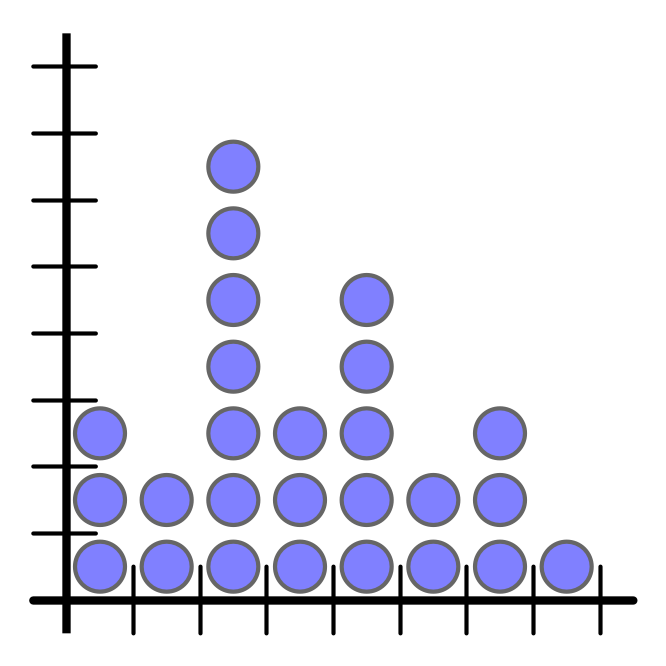
Packet Bundling Strategy, $C > 1$
- bundle groups of $C$ packets together
- treat bundles as individual packets
- ignore fractional part
-
apply protocol for $C = 1$ to bundles
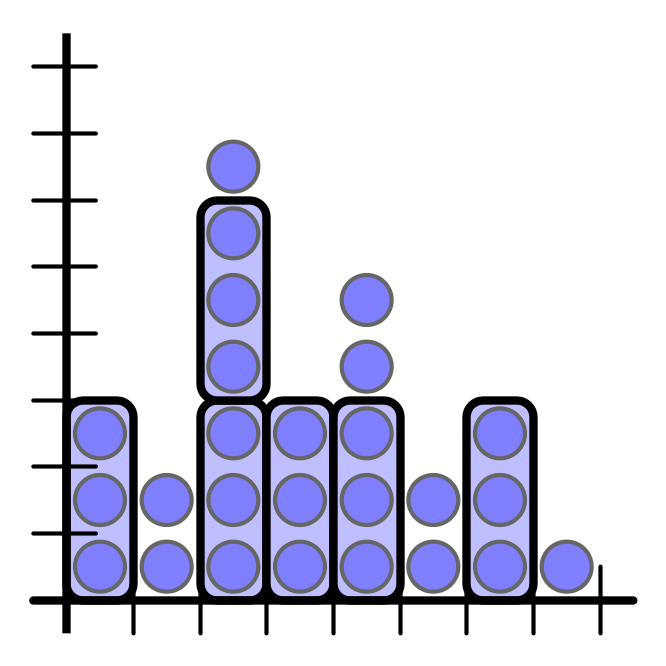
Packet Bundling Strategy, $C > 1$
- bundle groups of $C$ packets together
- treat bundles as individual packets
- ignore fractional part
-
apply protocol for $C = 1$ to bundles
Packet Bundling Strategy, $C > 1$
- bundle groups of $C$ packets together
- treat bundles as individual packets
- ignore fractional part
-
apply protocol for $C = 1$ to bundles
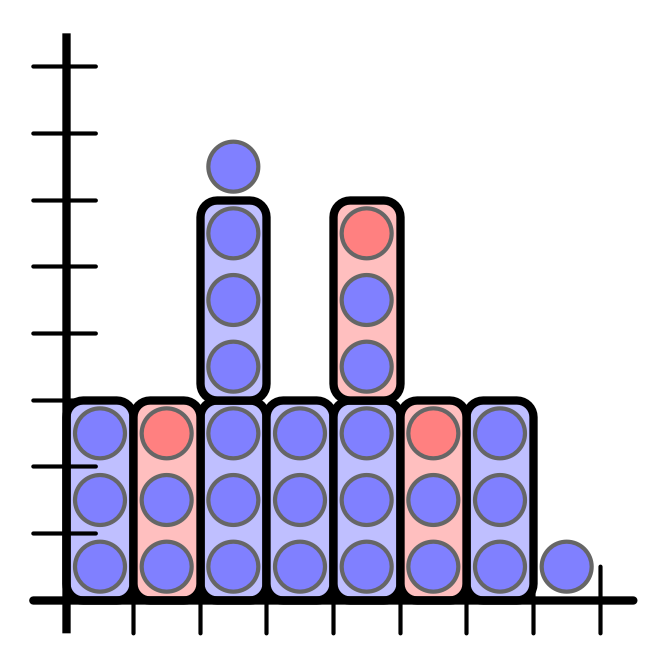
Bundling with an LBA
Theorem 1.
- consider bundling strategy
- original injection has parameters $\rho, \sigma, B$
- then arrival pattern of bundles is an LBA with parameters $\rho/C, \sigma/C, 1 + B / C$
Consequence. Any protocol/analysis for $C = 1$ can be applied to general $C$ as well.
- techniques can also be applied to heterogenous packet sizes
Note. Analogous results for AQT model do not hold.
Buffer Space Bounds for LBAs
Local Forwarding vs LBAs
Odd-Even Downhill Forwarding (OED). (Dobrev et al. + Patt-Shamir & R–). Each round, buffer $i$ forwards iff
- $L(i) > L(i+1)$, or
- $L(i) = L(i+1)$ and $L(i)$ is odd
Theorem 2. For any LBA with parameters $\rho \leq 1$, $\sigma, B \geq 1$, the buffer space requirement of OED is $O(B \log n + \sigma)$.
-
AQT analysis had $O(\log n + \sigma)$ for $\rho \leq 1$
-
Theorem 2 follows from more refined analysis of OED algorithm
Lower Bounds
Theorem 3. $P$ any (possibly centralized and/or randomized) forwarding protocol, $B, \sigma \geq 1$. Then there is an LBA such that $P$ requires $\Omega(B \log n + \sigma)$ buffer space.
Consequences.
- OED forwarding is asymptotically optimal for LBAs
- Locality/buffer space tradeoff disappears in LBA model
- For AQT model (P-S & R– 2019):
For protocols with locality $d$, buffer space $\Theta(1 + \frac 1 d \log n)$ is necessary and sufficient
- For LBA model: local is optimal!
- For AQT model (P-S & R– 2019):
Next Steps
- Consider more general topologies
- path with $k$ destinations requires $\Theta(k)$ buffer space (offline/centralized) even without bursts
- local solution for multiple destinations?
- Semi-synchronous model?
- results for continuous flows (in paper) may be relevant
- Locality vs Quality for other online problems?