Sampling Edges and More

Will Rosenbaum

Amherst College

Outline

1. Introductory Remarks
2. Sampling Edges: A Simple Algorithm
3. Optimality?
4. Parameterization by Arboricity
5. Applications and Open Questions

1. Introductory Remarks

About Me

Assistant Professor in CS at Amherst College

Previously:

• Postdocs at MPI for Informatics in Saarbrücken, Germany and Tel Aviv University
• Grad at UCLA (Math)

Generally interested in CS Theory: algorithms and complexity

• role of communication and locality in algorithms
  • local and distributed algorithms
  • sub-linear algorithms
• algorithms with uncertainty about input

A Large(?) Graph

Goal: Sample a Random Edge

Problem: Don’t Initially Know Edges

Computational Model

• $G = (V, E)$ a very large graph
• access to $G$ provided via queries:
  • sample a (uniformly random) vertex $v \in V$
  • degree query: return the degree of vertex, $d(v)$
  • neighbor query: return the $i$-th neighbor of $v$
  • pair query: return whether or not $(u, v) \in E$

A.k.a. general graph model in property testing

Problem Statement

Goal. Sample an edge $e \in E$ from an almost uniform distribution.

• use as few queries as possible

2. Sampling Edges: A Simple Algorithm

Warm-Up

What if an upper bound $\Delta$ on maximum degree is known?

A Graph with $\Delta = 4$

Pick a Random Vertex

Pick a Random Number \(\leq \Delta\): 3

Failure. Try Again!

Pick a Random Vertex

Pick a Random Number $\leq \Delta$: 2

Return Selected Edge

Simple Algorithm

What if an upper bound $\Delta$ on maximum degree is known?

1. pick vertex $v$ uniformly at random
2. pick a number $i$ from ${1, 2, \ldots, \Delta}$ uniformly at random
3. query $i$th neighbor of $v$
   • if a vertex $w$ is found, return $e = (v, w)$
   • otherwise, go to step 1

Question 1

Claim 2. Expected number of queries until success is $O\left(\frac{n \cdot \Delta}{m}\right)$.

For what graphs is this algorithm efficient?

Question 2

Claim 2. Expected number of queries until success is $O\left(\frac{n \cdot \Delta}{m}\right)$.

What if there is no (known) upper bound on maximum degree?

More Questions

Can we do better…

…when no bound on $\Delta$ is known?

…when $n \Delta / m$ is large?

Main Question. For what (families of) graphs can we sample edges efficiently?

• What promises ensure efficient edge sampling?

An Illustrative Example

Observe

• $\Delta = \Theta(n)$
• $m = \Theta(n)$
• $\implies n \Delta / m = \Theta(n)$
• can always sample with $\Theta(n)$ queries
  • get degrees of all vertices

Leaf Edges are Easy to Sample

See Middle Edge w/ Prob \(\Omega(1/n)\)?

Access Middle Vertices via Neighbors

Access Middle Vertices via Neighbors

Generalizing the Procedure

Technicalities

Edges \(\to\) Oriented Pair of Edges

Partition Vertices into Heavy/Light

Partition Edges into Heavy/Light

Another View

To Sample Light Edge

1. Sample Vertex; Check Light

2. Pick Random \(i \leq \theta\)

3. Return \(i\)th Edge (or Fail)

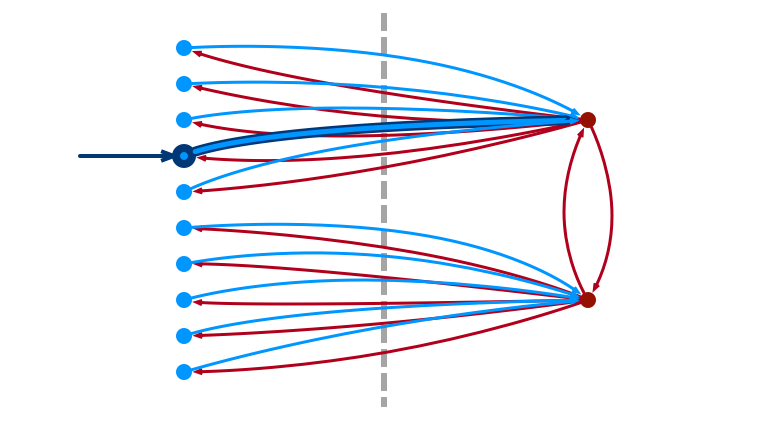
To Sample Heavy Edge

1. Sample Light Edge \((u, v)\)

2. If \(v\) is Light, Fail

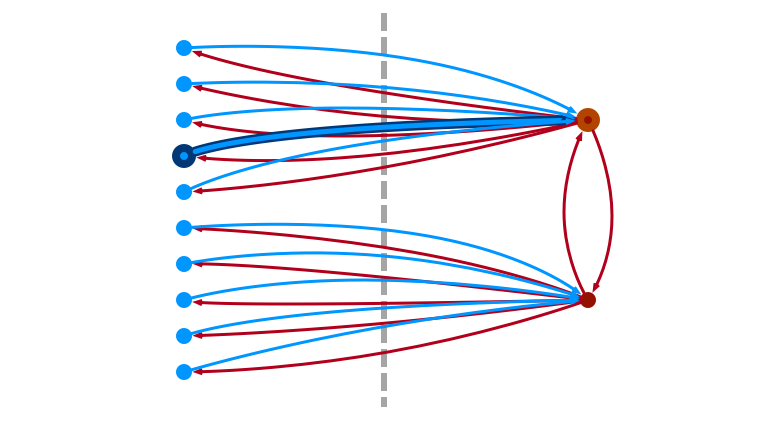
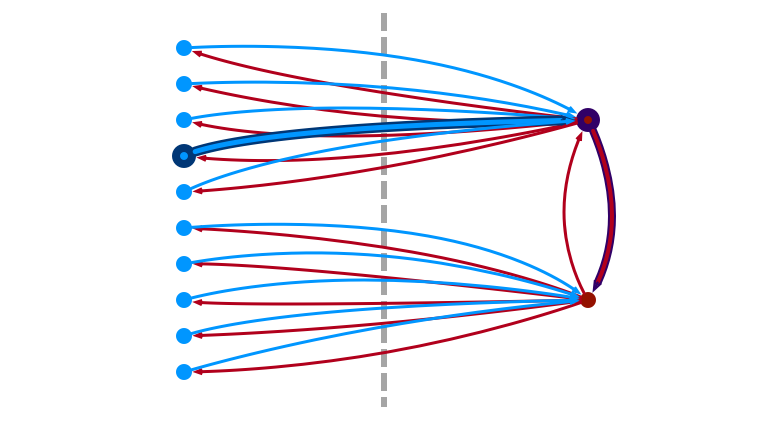
3. Otherwise, Pick Random Neighbor

Choosing Threshold \(\theta\)

Want:

1. $\theta$ as small as possible
   • want light edge sampling to succeed
2. every heavy vertex has mostly light neighbors
   • can reach every heavy vertex in one step from light
   • hit each heavy vertex with prob. proportional to its degree

A Good $\theta$

Choose:

• $\theta = \sqrt{m / \varepsilon}$
  • $m$ is number of oriented edges

An Issue?

We chose $\theta = \sqrt{m / \varepsilon}$

What is the problem with this?

The General Algorithm

Until an edge is sampled, flip a coin

• with probability 1/2, try to sample light edge
  • pick $u$ uniformly at random
  • if $u$ is light, pick random $i \leq \theta$ u.a.r.
  • if $i \leq d(u)$, return $(u, v)$ ($v$ is $i$th neighbor)
• with probability 1/2, try to sample heavy edge
  • try to sample light edge $(u, v)$
  • if $v$ is heavy, return random incident edge $(v, w)$

Analysis

Claim 1. Light edge procedure returns every light edge with probability $\frac{1}{n \cdot \theta}$. $\Box$

Proof of Claim 2.

Suppose $v$ is a heavy vertex, $d_L(v)$ the number of its light neighbors.

By Lemma (and choice of $\theta$), $d_L(v) \geq (1 - \varepsilon) d(v)$

Running Time

• probability of success is at least
  • $\frac{(1 - \varepsilon) m}{n \cdot \theta} \geq \frac{\sqrt{\varepsilon m}}{2 n}$

Main Result

Theorem. The general algorithm samples edges almost uniformly using $O\left(\frac{n}{\sqrt{\varepsilon m}}\right)$ queries in expectation.

3. Optimality?

Can We Do Better?

Question. Can we sample edges using $o\left(\frac{n}{\sqrt{m}}\right)$ queries?

No!

A Lower Bound

Theorem. Any algorithm that samples edges almost uniformly requires \(\Omega\left(\frac{n}{\sqrt{m}}\right)\) queries.

Is Lower Bound Construction Reasonable?

Eh, maybe not?

Easy Instance ($n = 24, m = 44$)

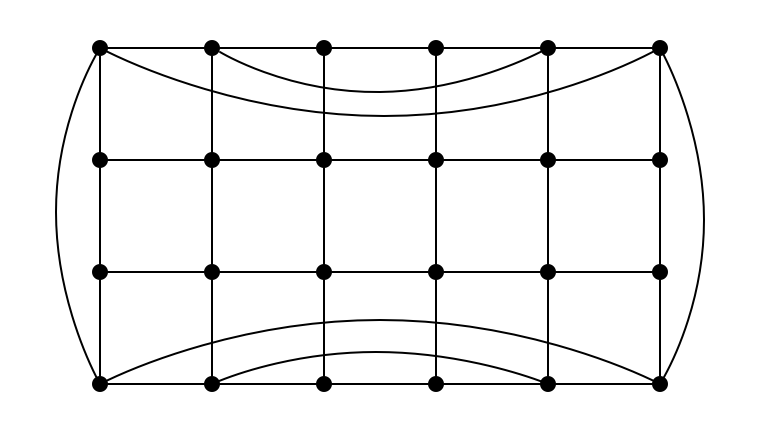
Hard Instance ($n = 24, m = 44$)

What Makes an Instance Hard?

4. Parameterization by Arboricity

What is Arboricity?

The arboricity of a graph $G$, denoted $\alpha(G)$ is:

1. the maximum average degree of any subgraph of $G$

2. the minimum number of spanning trees (forests) whose union is $G$

Theorem (Nash-Williams, 1964). The two definitions above are equivalent.

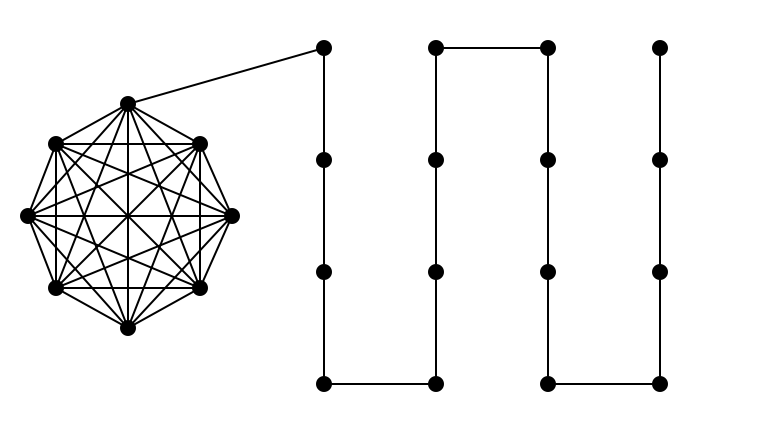
High $\Delta$, Small $\alpha$

High $\Delta$, Small $\alpha$, 1

High $\Delta$, Small $\alpha$, 2

High $\Delta$, Small $\alpha$, 3

Does Knowing Arboricity Help?

Intuition. If $\alpha \approx \frac{m}{n}$, then no subgraphs much denser than average

• no place to hide edges

But how to use this fact?

• before, our tricky instance was a tree—$\alpha = 1$…

Structural Lemma

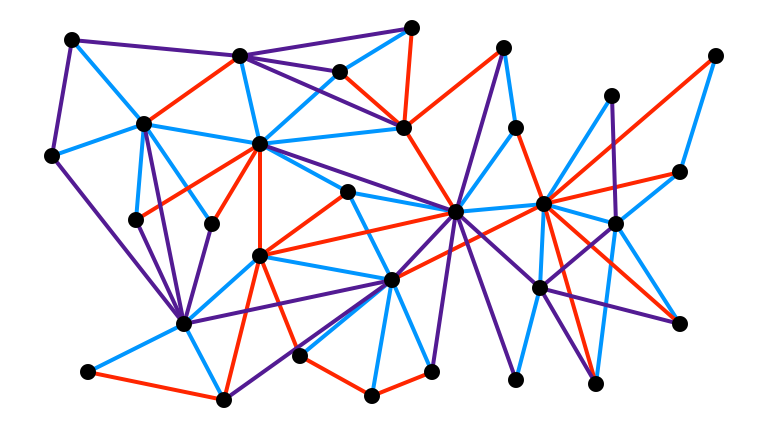
Lemma. If $G = (V, E)$ has arboricity at most $\alpha$, then $V$ can be partitioned into layers $L_0, L_1, \ldots, L_\ell$ with $\ell \leq \log n$ such that:

1. $v \in L_0 \iff v$ has degree at most $O(\alpha \log n)$,

2. every $v \in L_i$ with $i \geq 1$ has $1 - O(1/\log n)$ fraction of neighbors in $L_0, L_1, \ldots, L_{i-1}$.

Structural Lemma, Illustrated

Observation

Layered decomposition $\approx$ light/heavy decomposition from before

• can sample “light” edges (from $L_0$) easily
• to access heavy edges, start at $L_0$ and walk upwards
• all vertices reachable after $\leq \log n$ steps

An Algorithm

Repeat until successful:

1. use rejection sampling to sampling to sample a vertex $u \in L_0$ with probability proportional to its degree
   • note $u \in L_0 \iff d(u) \leq C \alpha \log n$
2. Pick $k \in {0,1,\ldots,\ell}$ uniformly at random.
3. Perform a simple random walk of length $k$ starting from $u$.
4. Abort if another vertex in $L_0$ is encountered.
5. If random walk ends at $v$, return $(v,w)$, where $w$ is a uniformly random neighbor of $v$.

Illustration

Pick Random $u$ in $L_0$ Prop. to $d(u)$

Pick Random $k$ in $\{0, 1, 2, 3\}$: 2

Random Walk Step $1$

Random Walk Step $2$

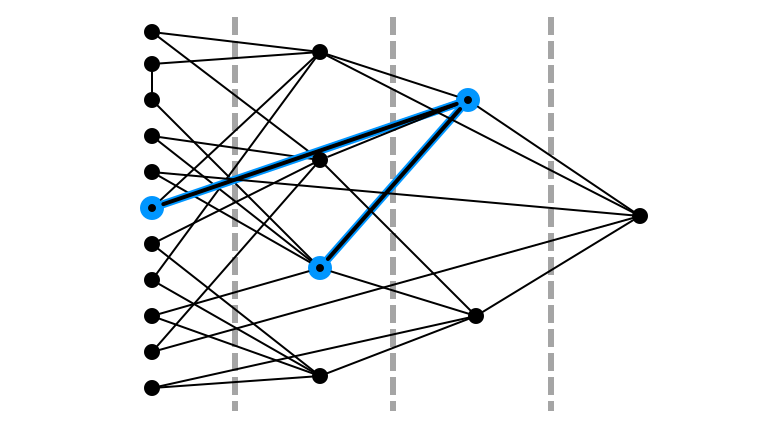
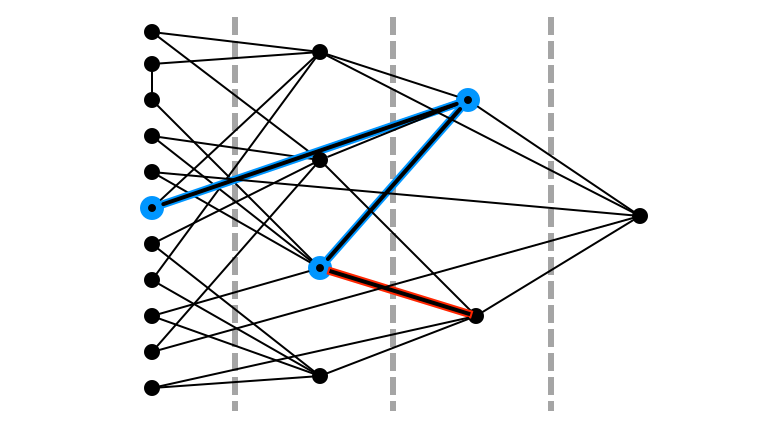
Didn’t Return to $L_0$

Return Random Incident Edge

Main Result

Theorem. A single iteration returns each edge $e \in E$ with probability $p(e)$ satisfying

• \((1 - \varepsilon) \frac{\varepsilon}{\alpha n \log^2 n} \leq p(e) \leq \frac{\varepsilon}{\alpha n \log^2 n}\).

Therefore, the procedure samples edges almost uniformly using $O^*\left(\frac{\alpha n}{m}\right)$ queries in expectation.

Interesting Feature

Observation. The layered decomposition doesn’t appear in the sampling algorithm!

• used to justify the algorithm
  • provides intuition about the random walk process
• decomposition appears in the analysis of the algorithm

5. Applications and Open Questions

Application of Technique: Sampling Cliques

What if we want to sample bigger subgraphs…not just single edges?

• E.g., sampling random triangles, 4-cliques, $k$-cliques

Application of Technique: Sampling Cliques

• Define auxuiliary graph $H_{k}$:
  • vertices in $H_{k}$ are $k-1$ cliques
  • when vertices in $H_k$ share an edge, edge corresponds to $k$-clique
  • sampling edges in $H_k$ corresponds to sampling $k$-cliques in $G$

Application of Technique: Sampling Cliques

Theorem. Almost uniformly random $k$-cliques can be sampled using $O^*\left(\frac{n \alpha^{k-1}}{n_k}\right)$ queries in expectation, where $n_k$ is the number of $k$-cliques in the graph.

• Upper bound is tight for wide range of parameters

Note. For $k > 2$, lower bound separates complexity of sampling and approximate counting!

• In bounded arboricity graphs, triangles can be approximately counted in $O^*(1)$ queries

Black Box Applications

Previous works employ edge samples for other tasks:

• Counting arbitrary graphs

• Sampling arbitrary graphs

Open Questions and Future Directions

1. Can we sample graphs other than cliques efficiently in low-arboricity graphs?

2. When do approximate queries suffice?
   • e.g., almost uniformly random edges instead of exactly uniform
3. What general relationships can we find between different query models?
   • recent papers introduce more exotic queries: IS, BIS, Inner Product,…
   • how can we understand the relative computational power of these primitives?

Thank You!

Any Questions?