Stable Matchings with Restricted Preferences: Structure & Complexity

Christine Cheng (University of Wisconsin, Milwaukee)

Will Rosenbaum (Amherst College)

Overview

1. Background
2. Main Results
3. Methods
4. Open Problems

Background

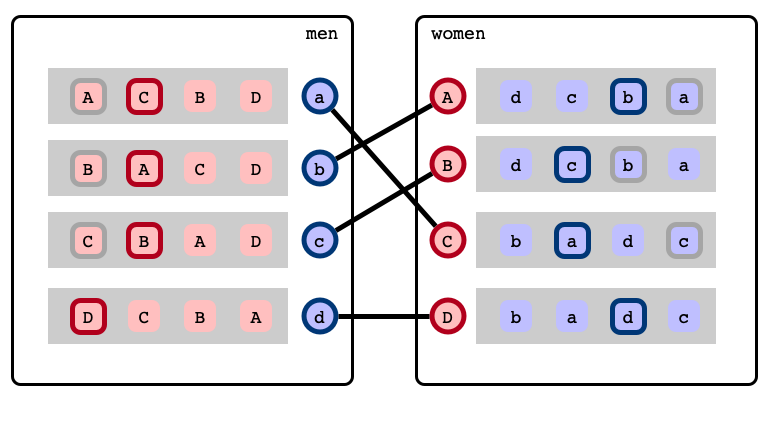
Stable Marriage Problem

Agents: traditionally, men and women

Stable Marriage Problem

Preferences

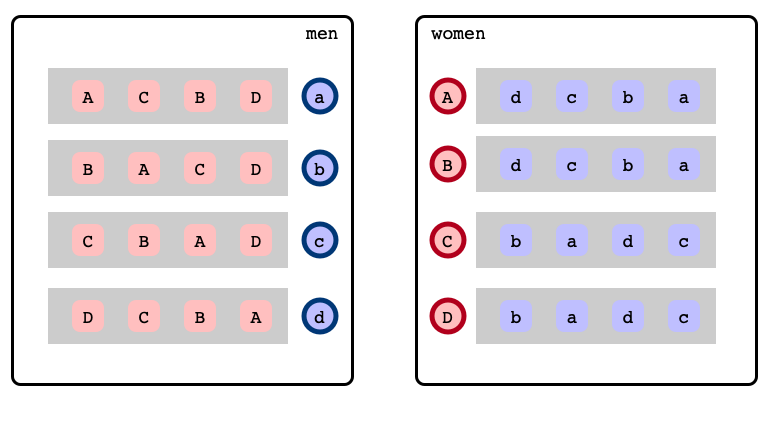
Stable Marriage Problem

A matching…

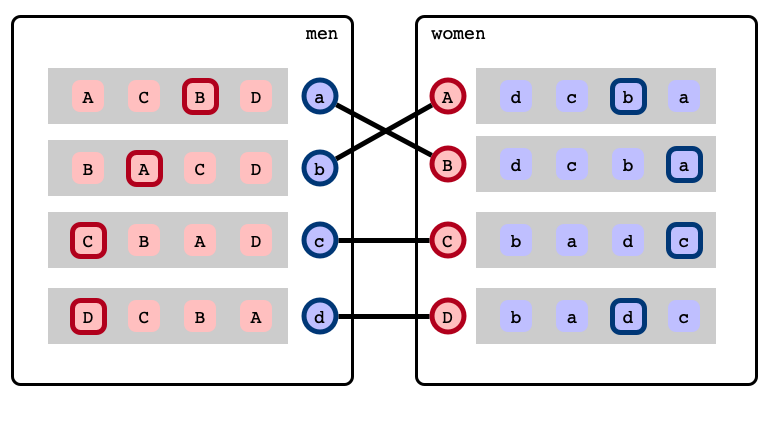
Stable Marriage Problem

… with a blocking pair

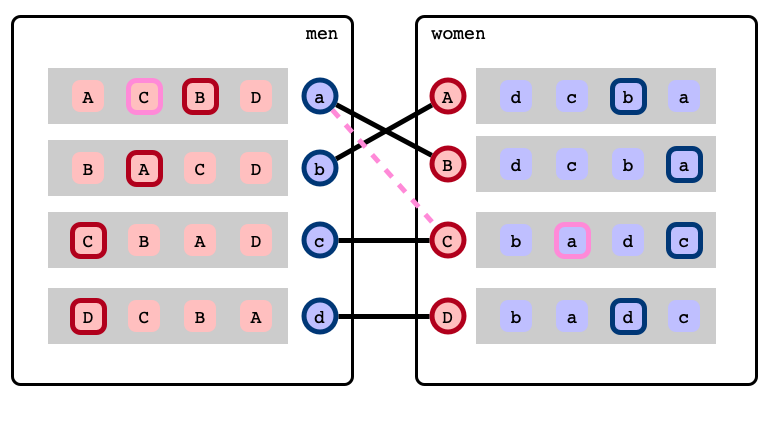
Stable Marriage Problem

A stable matching

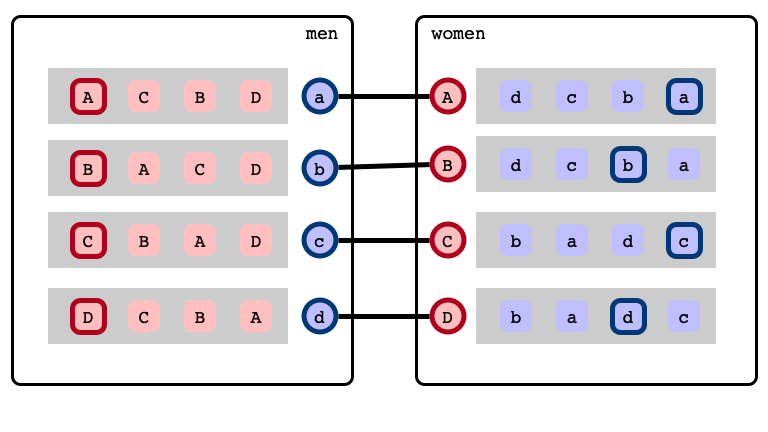
Gale-Shapley Algorithm

Gale & Shapley 1962:

• Efficient algorithm that finds a stable matching
  • stable matchings always exist!

Limitations of Gale-Shapley

• Finds at most two stable matchings
  • one optimal for men, pessimal for women
  • one optimal for women, pessimal for men
• Can be exponentially many stable matchings!

Questions

• How many stable matchings does an instance have?
• Can we find fair stable matchings?
  • median
  • balanced
  • sex-equal
  • …
• Can we sample a uniformly random stable matching?

To address these questions, must understand structure of stable matchings!

Rotations

A stable matching

Rotations

a’s next best choice

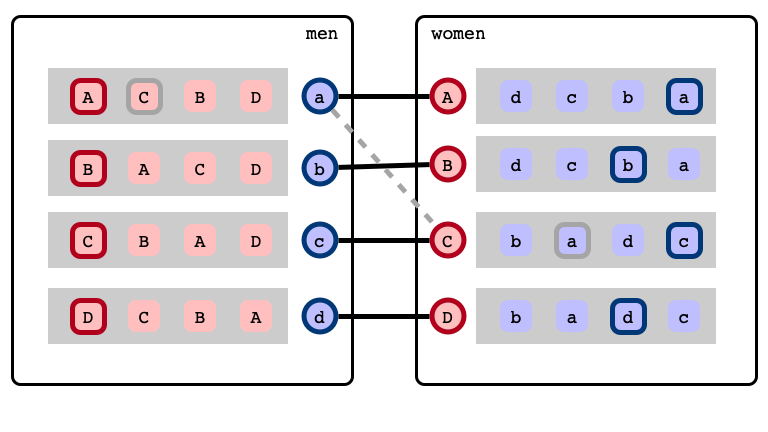
Rotations

c’s next best choice

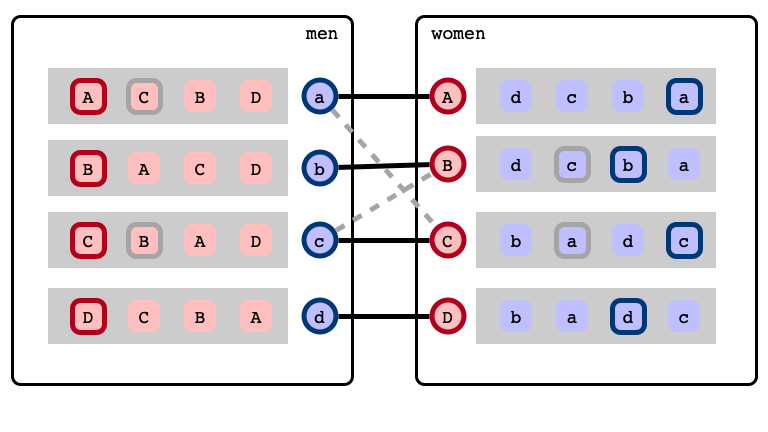
Rotations

b’s next best choice

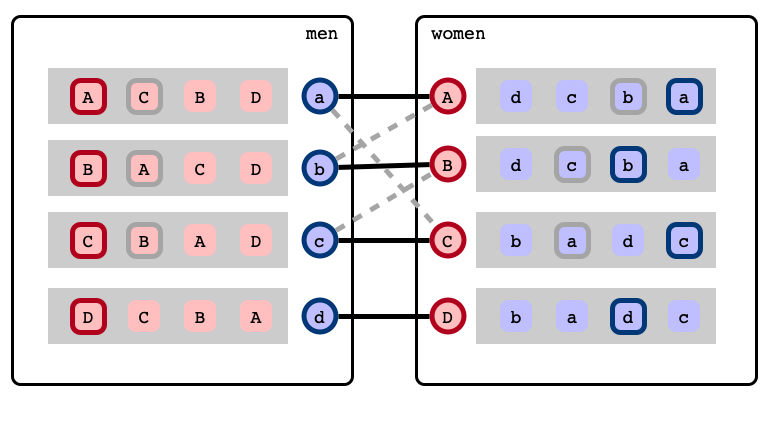
Rotations

Rotation exposed!

Rotations

Rotation eliminated—new SM found!

Structure of Stable Matchings

Irving & Leather, 1986:

• All stable matchings obtained by eliminating sequence of rotations
• Natural precedence relation on rotations: rotation poset
• Stable matchings one-to-one with downsets in rotation poset

Theorem (Irving & Leather, 1986):

1. Rotation posets can be efficiently computed
2. Every (finite) poset is a rotation poset

Structure and Complexity

The following problems are (NP)-hard:

• Counting stable matchings
• Finding median, balanced, and sex-equal stable matchings

Proof technique: reduction from equivalent (hard) problems on rotation poset

• Structure of rotation poset determines complexity of associated task

Question

Do hard SM instances arise in practice?

Restricted Preferences

We consider restricted preference models:

1. $k$-bounded
2. $k$-attribute
3. $(k_1, k_2)$-list
4. $k$-range

2–4 introduced by Bhatnagar et al. (SODA 2008)

$k$-Bounded Preferences

An SM instance is $k$-bounded if all preference lists have length at most $k$

Motivation. Rarely the case in practice that one would rank all possible partners!

$k$-Attribute Preferences

Each agent $a$ has a profile $(v_a, \phi_a)$

• $v_a \in \mathbf{R}^k$
• $\phi_a : \mathbf{R}^k \to \mathbf{R}$, linear
• $a$’s ranks potential partners $b$ according to $\phi_a(v_b)$

Motivation. Ranking by questionnaires (e.g., dating websites):

• $v_a$ encodes own responses
• $\phi_a$ encodes desired responses of ideal partner
• $k$ is number/dimensions of questions

$(k_1, k_2)$-list Preferences

• Men/women partitioned into $k_1$ / $k_2$ groups, respectively
• All agents in each group have identical preference lists

Motivation. Cases where preferences inferred from group identity

• E.g., all prospective CS majors adopt same rankings of universities

$k$-Range Preferences

• For each woman $w$, men’s rankings of $w$ differ by at most $k - 1$
• For each man $m$, women’s rankings of $m$ differ by at most $k - 1$

Motivation. Preference derived from “master preference lists,” but with some noise.

Main Question

What rotation posets are realized by restricted preference models?

• Can we exploit restricted preference structures to give efficient algorithms for (restricted instances of) NP-hard problems?

Main Results

Hardness Results

Theorem 1. Let $\mathcal{P}$ be an arbitrary finite poset. Then there exist SM instances in the following models realizing $\mathcal{P}$:

• $k$-bounded for any $k \geq 3$
• $k$-attribute for any $k \geq 6$
• $(k, \infty)$-list for any $k \geq 2$

Such instances can be computed from $\mathcal{P}$ in polynomial time.

Hardness Consequences

• Structural problems are as hard in the following models as the general case:
  • $k$-bounded for any $k \geq 3$
  • $k$-attribute for any $k \geq 6$
  • $(k, \infty)$-list for any $k \geq 2$
• For example:
  • counting stable matchings is #BIS-complete
  • finding median stable matchings is #P-hard

Algorithmic Results

Theorem 2. For constant $k$, the rotation poset of every $k$-range SM instance has bounded pathwidth.

• Structure of $k$-range rotation posets is highly restricted.

Theorem 3. Given a poset $\mathcal{P}$ with pathwidth $k$, can efficiently construct an $O(k)$-range SM instance realizing $\mathcal{P}$.

• Pathwidth characterizes $k$-range rotation posets

Algorithmic Consequences

For any constant $k$, and any $k$-range instance, we can efficiently

1. count and sample stable matchings
2. find median, balanced, and sex-equal stable matchings

These problems are NP-hard in general!

Takeaway Messages

1. For small constant $k$, $k$-bounded, $k$-attribute, and $(k, \infty)$-list preferences realize all finite posets
   • structural problems are as hard as for general instances
2. For all constant $k$, $k$-range preference have highly restricted rotation posets
   • computational problems may be significantly easier than the general case

Methods

Constructions

Goal. Given a poset $\mathcal{P}$, construct an SM instance with

1. rotation poset isomorphic to $\mathcal{P}$, and
2. preferences from a (chosen) restricted family

Start with Rotations

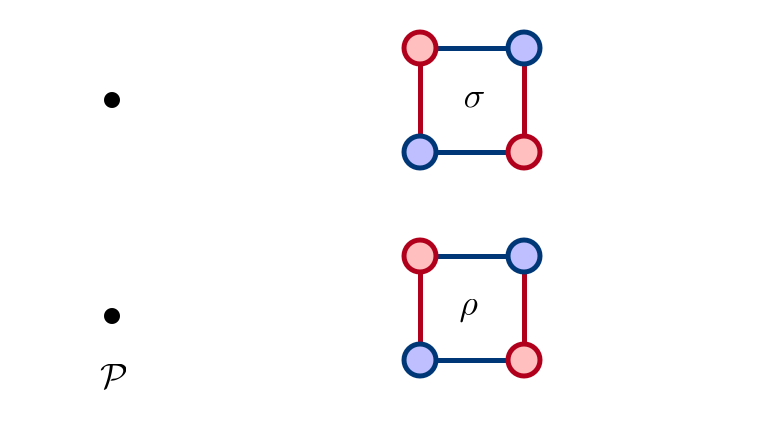
SM 1: Man Optimal

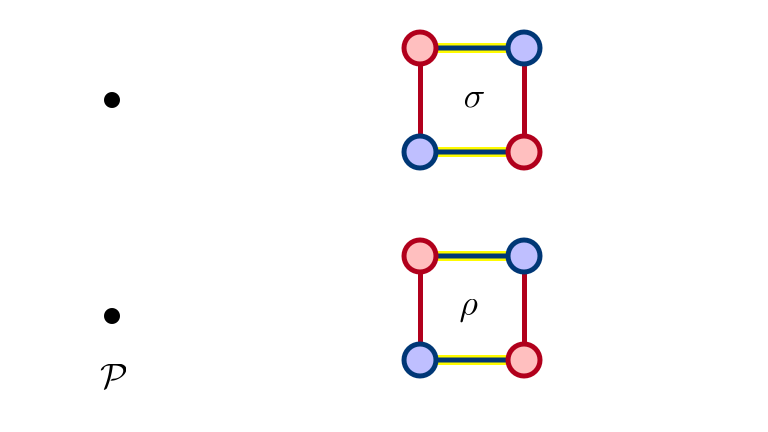
SM 2: $\rho$ Eliminated

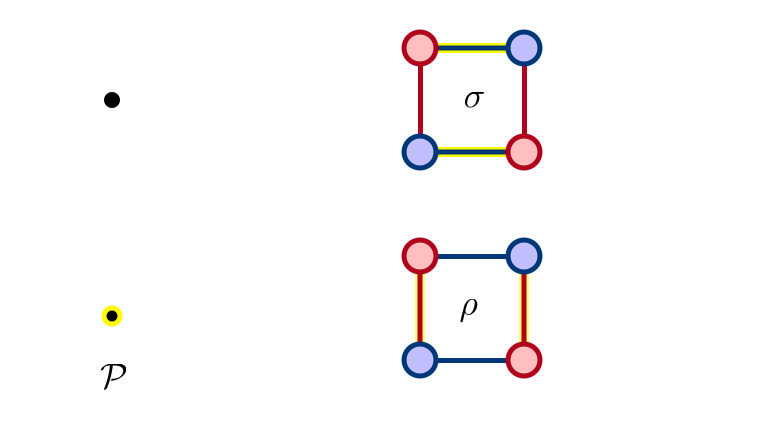
SM 3: $\sigma$ Eliminated

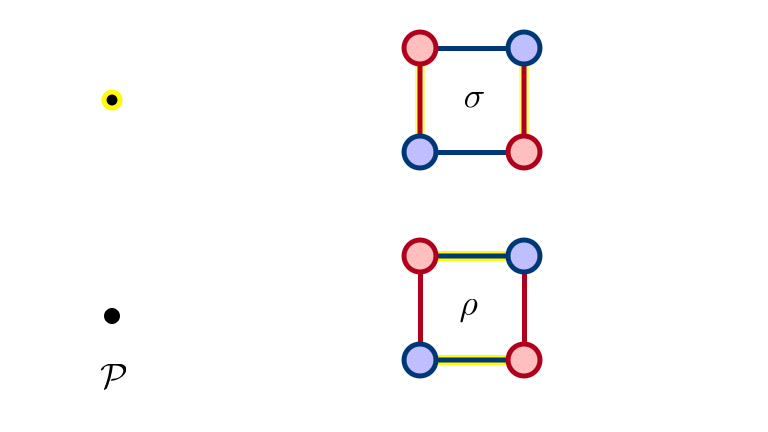
SM 4: $\rho, \sigma$ Eliminated

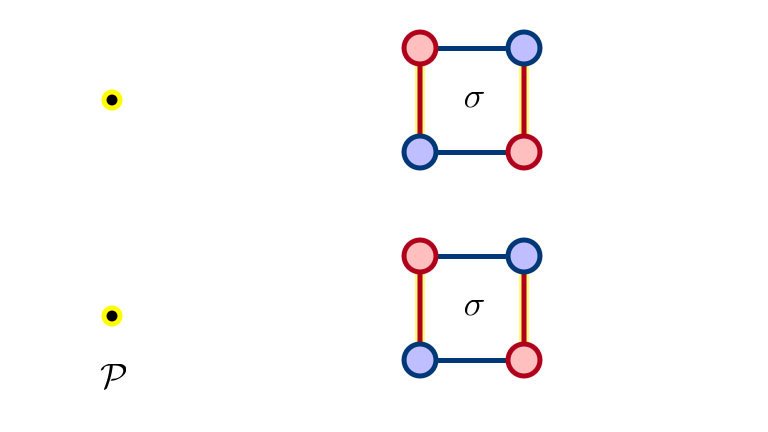
Adding Edge

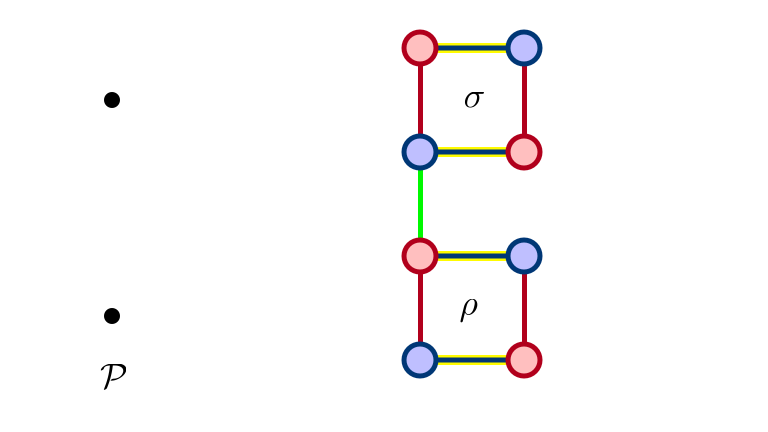
$\sigma$ Not Exposed…

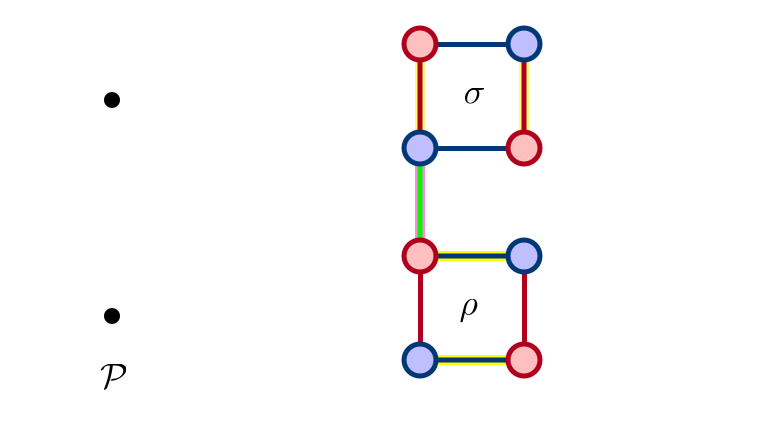
$\sigma$ Exposed After $\rho$ Eliminated

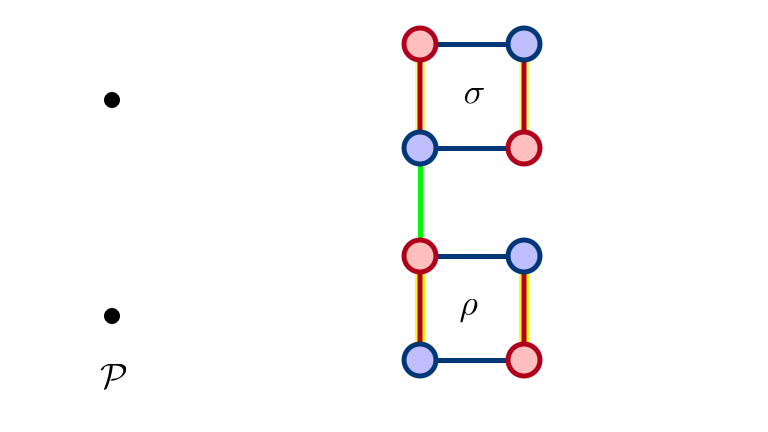
Added Precedence

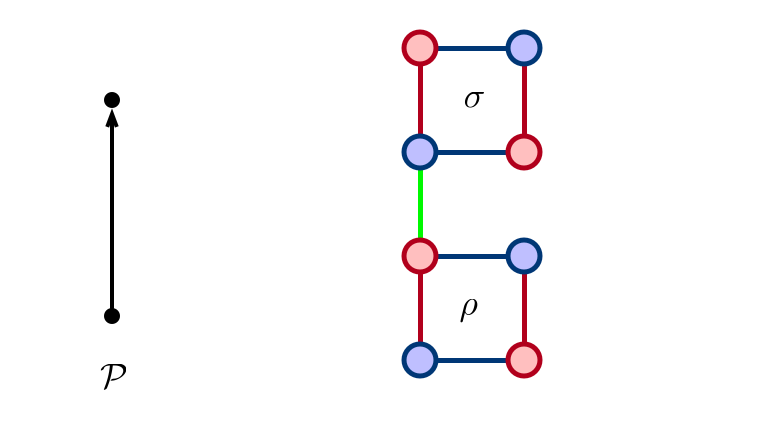
Larger Construction

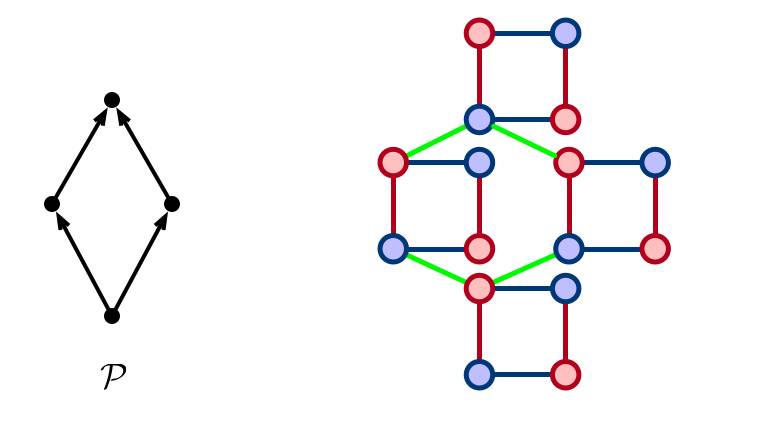
Paper Constructions

• Formalize “glueing” together rotations to force precedence
• Generic construction
  • each poset $\implies$ many instances realizing poset
  • construct instances in preference models

Open Problems

1. Structure of rotation posets for $(k_1, k_2)$-list preferences ($k_1, k_2 < \infty$)?
2. Generalizations to preferences with ties/indifference?
3. Structure of stable matchings on restricted graph families (e.g., planar, bounded genus, …)?

Thank You