Stable Matchings with Restricted Preferences: Structure & Complexity

Christine Cheng (University of Wisconsin, Milwaukee)

Will Rosenbaum (Amherst College)

Stable Marriage Problem

Agents: traditionally, men and women…

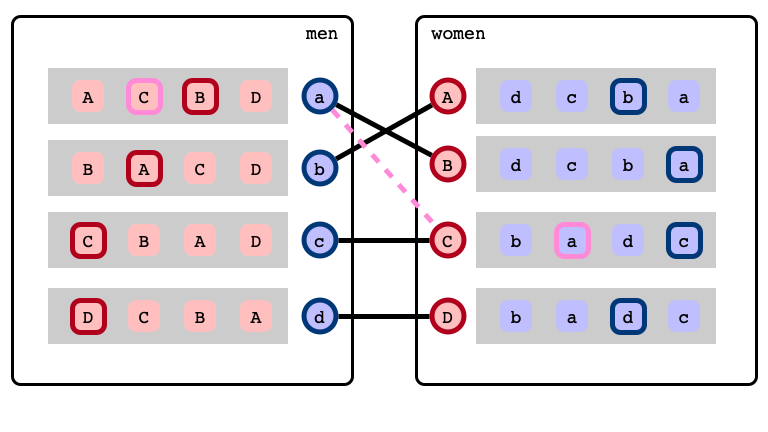
agents

Stable Marriage Problem

A stable matching

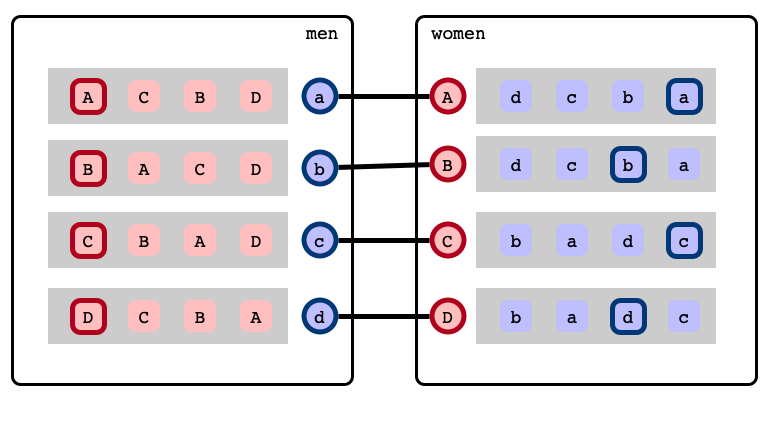
agents

Gale-Shapley Algorithm

Gale & Shapley 1962:

  • Efficient algorithm that finds a stable matching
    • stable matchings always exist!

Intractible Problems

  • How many stable matchings does an instance have?
  • Can we find fair stable matchings?
    • median
    • balanced
    • sex-equal

Restricted Preferences

We consider restricted preference models:

  1. $k$-bounded
  2. $k$-attribute
  3. $(k_1, k_2)$-list
  4. $k$-range

2–4 introduced by Bhatnagar et al. (SODA 2008)

Main Results

  1. Characterize structure of stable matchings for preference models
  2. $k$-bounded, $k$-attribute, $(k, \infty)$-list give generic structure
    • intractible structural problems remain intractible
  3. $k$-range instances have highly restricted structure
    • fast algorithms for many problems

To Learn More

Stable Matchings with Restricted Preferences: Structure and Complexity